Physicist3
- 103
- 0
http://www.flickr.com/photos/53512951@N06/8229416013/in/photostream/
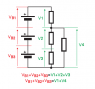
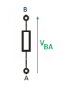
With regards to the circuit in the image linked above, I have been told to start in the bottom left hand corner and then work clockwise around the circuit, adding up all the voltages to see if they follow the KVL principle. The thing is, the arrows and polarity is confusing me a bit. Should it be -Vs + V1 + V2 = 0, or Vs - V1 - V2 = 0? Could someone explain which one is correct and what the arrows represent please? Thanks :)
With regards to the circuit in the image linked above, I have been told to start in the bottom left hand corner and then work clockwise around the circuit, adding up all the voltages to see if they follow the KVL principle. The thing is, the arrows and polarity is confusing me a bit. Should it be -Vs + V1 + V2 = 0, or Vs - V1 - V2 = 0? Could someone explain which one is correct and what the arrows represent please? Thanks :)