Anavra
- 4
- 0
Apologies if this is too basic, but I've been studying for a while and I'm stuck.
Spring paradox. What is wrong with the following argument?
Consider a mass m held at rest at y = 0, the end of
an unstretched spring hanging vertically. The mass is now
attached to the spring, which will be stretched because of the
gravitational force mg on the mass. When the mass has lost
gravitational potential energy mgy and the spring has gained
the same amount of potential energy so that
mgy= 1/2 cy2
the mass will come to equilibrium. Therefore the position of
equilibrium is given by
y= (2mg)/C
Conservation of total mechanical energy
K_1 + U_1 = K_2 + U_2
Potential Energy (gravitational)
U=mgy
Potential Energy (elastic)
1/2 cy2
Kinetic Energy
1/2 mv2
At first glance, I can't seem to figure out what is wrong with the argument. So I began recreating the whole thing.
I started drawing it this way:
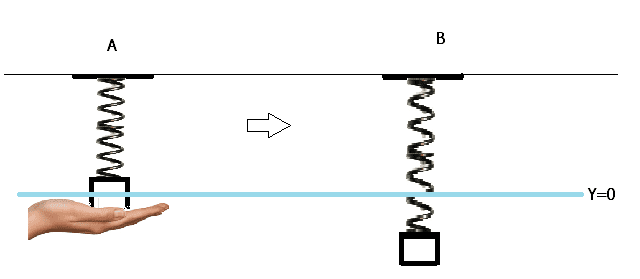
A is the intial situation where the spring is at rest, not supporting the mass. It's just there.
B is the situation where the mass has been attached to the spring which supports the mass' weight. The blue line depicts y=0.
Since no non-conservative forces seem to be involved here, I applied the conservation of total mechanical energy, this makes:
EA=EB
KA+UA=KB+UB
Since the A situation is at the assigned zero, both elastic potential and gravitational potential will be 0. It's at rest so kinetic is also 0. In short, EA=0
0=1/2 cy2 - mgy + 1/2 mv2
The spring would go up and down and eventually reach equilibrium, where the kinetic energy is zero.
0=1/2 cy2 - mgy
So far nothing wrong has been found about the problem given. Because this leads to:
mgy=1/2 cy2
And then, solving for y, it becomes
y= (2mg)/C
Again, this matches the results given. So I can't find what's wrong. Is it a trick question and nothing is wrong? Am I missing something? Thanks!
Homework Statement
Spring paradox. What is wrong with the following argument?
Consider a mass m held at rest at y = 0, the end of
an unstretched spring hanging vertically. The mass is now
attached to the spring, which will be stretched because of the
gravitational force mg on the mass. When the mass has lost
gravitational potential energy mgy and the spring has gained
the same amount of potential energy so that
mgy= 1/2 cy2
the mass will come to equilibrium. Therefore the position of
equilibrium is given by
y= (2mg)/C
Homework Equations
Conservation of total mechanical energy
K_1 + U_1 = K_2 + U_2
Potential Energy (gravitational)
U=mgy
Potential Energy (elastic)
1/2 cy2
Kinetic Energy
1/2 mv2
The Attempt at a Solution
At first glance, I can't seem to figure out what is wrong with the argument. So I began recreating the whole thing.
I started drawing it this way:
A is the intial situation where the spring is at rest, not supporting the mass. It's just there.
B is the situation where the mass has been attached to the spring which supports the mass' weight. The blue line depicts y=0.
Since no non-conservative forces seem to be involved here, I applied the conservation of total mechanical energy, this makes:
EA=EB
KA+UA=KB+UB
Since the A situation is at the assigned zero, both elastic potential and gravitational potential will be 0. It's at rest so kinetic is also 0. In short, EA=0
0=1/2 cy2 - mgy + 1/2 mv2
The spring would go up and down and eventually reach equilibrium, where the kinetic energy is zero.
0=1/2 cy2 - mgy
So far nothing wrong has been found about the problem given. Because this leads to:
mgy=1/2 cy2
And then, solving for y, it becomes
y= (2mg)/C
Again, this matches the results given. So I can't find what's wrong. Is it a trick question and nothing is wrong? Am I missing something? Thanks!