Is Gravitational Attraction Negligible in Oscillating Systems?

[Saitama]

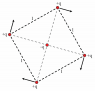
Homework Statement

Homework Equations

The Attempt at a Solution

I have tried to attack this problem with two methods but no luck. I always end up with something gibberish. :/

Method 1:
Considering the forces on anyone charge, the net force on a charge is -\frac{kq^2(3\sqrt{2}-4)}{4\sqrt{2}r^2}
hence,
ma=-\frac{kq^2(3\sqrt{2}-4)}{4\sqrt{2}r^2}
where $a=\frac{d^2r}{dt^2}$, this leads to a differential equation of the form
\frac{d^2r}{dt^2}=-\frac{k}{r^2}
where k is some constant. Plugging this in wolfram alpha gives me nothing. :(

Method 2:
Throughout the motion, energy and angular momentum is conserved. The potential energy of charges at any instant is
-\frac{kq^2(3\sqrt{2}-4)}{\sqrt{2}r}
Let the velocity of charge along the radius vector be $v_r$ and perpendicular to radius vector is $v_p$. Hence, the total kinetic energy is
4\left(\frac{1}{2}m(v_r^2+v_p^2)\right)
The total energy of the system at any time t is
E=-\frac{kq^2(3\sqrt{2}-4)}{\sqrt{2}r}+2m(v_r^2+v_p^2)
I don't really know what to do with this. Usually, in SHM problems, I would differentiate the expression for energy wrt time and set the derivative to zero but doing so here doesn't seem helpful. I can make one from equation from the fact that $dL/dt=0$ where L is the angular momentum of the system. L at any time is $4mv_pr$. Even if I differentiate the expression for L, I will end up with an equation which doesn't look useful.

Any help is appreciated. Thanks!

 

[mfb]

How did you get your equation for the force?

The motion in a 1/r^2-potential is called Kepler problem (he studied it for gravity), I guess you can use the formulas for that.It is amazing that such a system can exist (even if it is unstable).

 

[rude man]

My inclination is to solve the problem assuming L = constant = L0. The fact that the oscillations in L are not at all defined in terms of L(t) leads me to suspect that the net centripetal force on each +q charge is independent of L. That problem is pretty straight-forward.

However, I'm too lazy to prove that centripetal force is not a function of L.

 

[Saitama]

How did you get your equation for the force?

That's the net force in the radial direction on a single charge. Do I have to consider the centrifugal force too?

 

[WannabeNewton]

What happens to the radial velocity at the instants of maximum and minimum elongation of the sides of the square?

 

[Saitama]

What happens to the radial velocity at the instants of maximum and minimum elongation of the sides of the square?

It becomes zero.

 

[ehild]

dr/dt = 0 when the sides are Lo or 1/4 Lo. Lo is given in the problem. Use conservation or energy and angular momentum for these configurations.

ehild

 

[WannabeNewton]

It becomes zero.

Ok now use conservation law(s) for those instants. See where that takes you.

EDIT: darn it ehild. >.>

 

[ehild]

You were not present yet when I started to solve the problem and post. You were quicker, do it further.

ehild

 

[WannabeNewton]

You were not present yet when I started to solve the problem and post. You were quicker, do it further.

It was a joke xD <3

 

[Saitama]

dr/dt = 0 when the sides are Lo or 1/4 Lo. Lo is given in the problem. Use conservation or energy and angular momentum for these configurations.

ehild

$$E_i=-\frac{kq^2(3\sqrt{2}-4)}{L_0/4}+2mv_{pi}^2$$
$$E_f=-\frac{kq^2(3\sqrt{2}-4)}{L_0}+2mv_{pf}^2$$
Equating them
\frac{3kq^2(3\sqrt{2}-4)}{L_0}=2m(v_{pi}^2-v_{pf}^2)
Using conservation of angular momentum at these two instants,
4mv_{pi}\frac{L_0}{4\sqrt{2}}=4mv_{pf}\frac{L_0}{\sqrt{2}} \Rightarrow v_{pi}=4v_{pf}

Substituting the relation in energy in energy equation and solving for $v_{pf}^2$,
v_{pf}^2=\frac{kq^2(3\sqrt{2}-4)}{10mL_0}

What should I do with this?

 

[ehild]

Read the problem text again

How are vpi and vpf related to the angular speed and Lo?

ehild

 

[Saitama]

Read the problem text again

ehild

I still don't get it. The problem asks the time period of oscillation but what I have is the square of final velocity.

$v_p$ is the component of velocity perpendicular to the radius vector. $v_{pi}$ is the initial and $v_{pf}$ is the final.

$v_{pf}=\omega L_0/\sqrt{2}$?

 

[ehild]

I still don't get it. The problem asks the time period of oscillation but what I have is the square of final velocity.

$v_p$ is the component of velocity perpendicular to the radius vector. $v_{pi}$ is the initial and $v_{pf}$ is the final.

$v_{pf}=\omega L_0/\sqrt{2}$?

Yes, v_pf=ω_fL₀/√2. So you know the maximum and minimum ω, but I have to think about the time period...

ehild

 

[TSny]

Considering the forces on anyone charge, the net force on a charge is -\frac{kq^2(3\sqrt{2}-4)}{4\sqrt{2}r^2}

I agree with your expression for the force.

where $a=\frac{d^2r}{dt^2}$

In polar coordinates, the radial acceleration is not \ddot{r} but rather $\ddot{r}-r\dot{\theta}^2$.

The net force on a particle is an inverse square force. So, each particle travels an ellipse. I would follow mfb here. One of Kepler's laws should get you the answer straight away.

 

[WannabeNewton]

TSny mentioned Kepler's 3rd law, so you could roll with that and get the answer in a direct fashion analogous to the case for gravitational interactions. Since you already got the final angular velocity $\omega_{f}$, you could also use $r^{2}_{f}\omega_{f} = \frac{2\pi}{P}ab$ where $P$ is the period and $a,b$ are the semimajor and semiminor axes of the elliptical orbit (which you are given in the problem statement) of anyone of the charges respectively if you want: http://en.wikipedia.org/wiki/Kepler's_laws_of_planetary_motion#Second_law

 

[Saitama]

In polar coordinates...

Is there no other way?

The net force on a particle is an inverse square force. So, each particle travels an ellipse. I would follow mfb here. One of Kepler's laws should get you the answer straight away.

Kepler's third law?

 

[Saitama]

TSny mentioned Kepler's 3rd law, so you could roll with that and get the answer in a direct fashion analogous to the case for gravitational interactions. Since you already got the final angular velocity $\omega_{f}$, you could also use $r^{2}_{f}\omega_{f} = \frac{2\pi}{P}ab$ where $P$ is the period and $a,b$ are the semimajor and semiminor axes of the elliptical orbit of anyone of the charges respectively if you want: http://en.wikipedia.org/wiki/Kepler's_laws_of_planetary_motion#Second_law

How do I find a and b here?

Are they simply $L_0/\sqrt{2}$ and $L_0/4\sqrt{2}$?

 

[WannabeNewton]

The semimajor axis is the arithmetic average of the min and max position and the semiminor is the geometric average. I think it would be much easier to just go with what TSny said and just use Kepler's 3rd law. It's (Kepler's 3rd law) is usually written down in terms of the gravitational attraction but the potential here is essentially the same, just with different constants, so you would just have to adjust that part.

EDIT: By the way, by arithmetic average I meant $a = (r_f + r_i) /2$ and by geometric average I meant $b = (r_f r_i)^{1/2}$

 

[Saitama]

What is $r_f$ then? Is it equal to $a$?

 

[TSny]

How do I find a and b here?

Are they simply $L_0/\sqrt{2}$ and $L_0/4\sqrt{2}$?

No, those are not the lengths of the semi-major and semi-minor axes. They are the greatest and least distances to the central charge.

 

[Saitama]

No, they are not the lengths of the semi-major and semi-minor axes. They are the greatest and least distances to the central charge.

I am still confused. Why the path of the charges is an ellipse? Shouldn't they travel in a circle with a changing radius? This is how I analysed the situation before posting the problem here.

 

[ehild]

What can be a circle with periodically changing radius? :)

 

[TSny]

I am still confused. Why the path of the charges is an ellipse? Shouldn't they travel in a circle with a changing radius? This is how I analysed the situation before posting the problem here.

A circle with a changing radius?

The motion of a particle acted on by an inverse square attractive force must be a conic section.

 

[WannabeNewton]

I am still confused. Why the path of the charges is an ellipse? Shouldn't they travel in a circle with a changing radius? This is how I analysed the situation before posting the problem here.

To put it another way, there is a maximum distance from the stationary charge that each of the orbiting charges reach and there is a minimum distance from the stationary charge that they reach. For the given potential, we can have an elliptic (which includes circular), parabolic, or hyperbolic trajectory. Here we have a periodic orbit with each charge having a maximum distance from the central chatge (apoapsis) and minimum distance from the central charge (periapsis) so we have an elliptical orbit.

 

[Saitama]

From Kepler's third law
P^2 \propto a^3 \Rightarrow P^2=ka^3
where $a=(L_0/\sqrt{2}+L_0/(4\sqrt{2}))/2=5L_0/(8\sqrt{2})$ and k is some constant.

How should I determine k here?

I discussed a similar question before where I had to find this k. Please look at this thread: https://www.physicsforums.com/showthread.php?t=700759 (post #5) Can I use the same way here?

 

[ehild]

Use the second law.

 

[Saitama]

Use the second law.

$a=5L_0/(8\sqrt{2})$, $b=L_0/(2\sqrt{2})$
$r_f=L_0/\sqrt{2}$, $\omega_f=\sqrt{2\times 10^3 (3\sqrt{2}-4)}$

Plugging them in $r^{2}_{f}\omega_{f} = \frac{2\pi}{P}ab$
\frac{L_0^2}{4}\sqrt{2\times 10^3 (3\sqrt{2}-4)}=\frac{2\pi}{P}\frac{5L_0^2}{32}
Solving for P, $P=0.178 sec$. Looks good?

 

[mfb]

That's the net force in the radial direction on a single charge. Do I have to consider the centrifugal force too?

No centrifugal force. How did you arrive at those numbers?

 

[ehild]

$a=5L_0/(8\sqrt{2})$, $b=L_0/(2\sqrt{2})$
$r_f=L_0/\sqrt{2}$, $\omega_f=\sqrt{2\times 10^3 (3\sqrt{2}-4)}$

Plugging them in $r^{2}_{f}\omega_{f} = \frac{2\pi}{P}ab$
\frac{L_0^2}{4}\sqrt{2\times 10^3 (3\sqrt{2}-4)}=\frac{2\pi}{P}\frac{5L_0^2}{32}
Solving for P, $P=0.178 sec$. Looks good?

The area is correct. Show details of getting ω_f. The formula for vpf in #11 was still correct.

ehild