ladil123
- 42
- 0
Hello!
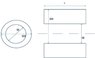
I want to calculate the stress in a ring that is mounted on a solid shaft due to the difference in temperature.
The temperature in the shaft is always higher than the temperature in the ring. The geometry is known, the shaft has a certain diameter and the outer diameter is also know.E-modulus and the thermal coefficient alpha is also known.
I just want to do a simple conservative estimate on the stress in the ring.
Thankful for any help with formulas etc.
Daniel
I want to calculate the stress in a ring that is mounted on a solid shaft due to the difference in temperature.
The temperature in the shaft is always higher than the temperature in the ring. The geometry is known, the shaft has a certain diameter and the outer diameter is also know.E-modulus and the thermal coefficient alpha is also known.
I just want to do a simple conservative estimate on the stress in the ring.
Thankful for any help with formulas etc.
Daniel
Last edited by a moderator: