nateja
- 33
- 0
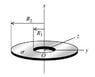
A thin disk with a circular hole at its center, called an annulus, has inner radius R_1 and outer radius R_2 (there's a picture which I will try to describe as best I can at the end of question). The disk has a uniform positive surface charge density δ on its surface. (a) determine the total electric charge on the annulus. (b) The annulus lies in the yz-plane, with its center at the origin. For an arbitrary point on the x-axis (the axis of the annulus), find the magnitude and direction of the electric field E (bold for vectors). Consider points both above and below the annulus.
there's more but for now I just need help on part b. The picture was this: http://www.cramster.com/answers-aug-09/physics/field-uniformly-charged-thin-disk-circular-hole-center-called-anann_633159.aspx?rec=0
δ = Q/A(area)
E = 1/(4*π*ε_0) * ((δ*A)/(R)^2)
Part A was easy, I thought, just:
Q = δ*A = δ*((2π(R_2)^2)-(2π(R_1)^2))
Then Part B (I'll try to explain in as clear terms as possible).
I divided the annulus into rings of area (2π(dR)^2)-(2π(R_1)^2). dR being an infinitely small distance for the 'outer radius.'
I set E = 1/(4*π*ε_0) * ((δ*(2π(dR)^2)-(2π(R_1)^2))/(dR + R_1)^2)
and then tried to doubled integrate. I used the bounds of the first integral for the ring as [R_1, R_2] and the second integral from [0,dwidth] for the annulus part. (I haven't been taught double integration yet, by the way - just a thing the university does - so I'm trying to figure it out as I go along)
I believe I have to use a dh (height) term in here somewhere and can I even do (dR)^2? Would this problem be better solved with thin slices with a d∅ term? I just did this problem: http://www.cramster.com/answers-sep-11/physics/semicircle-radius-quadrant_1485829.aspx?rec=0 .
So for a annulus, would I just need to use a full circle and double integrate to account for the thickness? That seems logical, but how do you go about adding another dimension to the problem... implicit differentiation??
there's more but for now I just need help on part b. The picture was this: http://www.cramster.com/answers-aug-09/physics/field-uniformly-charged-thin-disk-circular-hole-center-called-anann_633159.aspx?rec=0
Homework Equations
δ = Q/A(area)
E = 1/(4*π*ε_0) * ((δ*A)/(R)^2)
The Attempt at a Solution
Part A was easy, I thought, just:
Q = δ*A = δ*((2π(R_2)^2)-(2π(R_1)^2))
Then Part B (I'll try to explain in as clear terms as possible).
I divided the annulus into rings of area (2π(dR)^2)-(2π(R_1)^2). dR being an infinitely small distance for the 'outer radius.'
I set E = 1/(4*π*ε_0) * ((δ*(2π(dR)^2)-(2π(R_1)^2))/(dR + R_1)^2)
and then tried to doubled integrate. I used the bounds of the first integral for the ring as [R_1, R_2] and the second integral from [0,dwidth] for the annulus part. (I haven't been taught double integration yet, by the way - just a thing the university does - so I'm trying to figure it out as I go along)
I believe I have to use a dh (height) term in here somewhere and can I even do (dR)^2? Would this problem be better solved with thin slices with a d∅ term? I just did this problem: http://www.cramster.com/answers-sep-11/physics/semicircle-radius-quadrant_1485829.aspx?rec=0 .
So for a annulus, would I just need to use a full circle and double integrate to account for the thickness? That seems logical, but how do you go about adding another dimension to the problem... implicit differentiation??