scott_alexsk
- 335
- 0
Hello, (edit should be regular polygons in title)
I have been thinking a lot recently about 3D shapes formed by 2D regular polygons. I was asking myself if there would be any way to calculate the minimium number of regular polygons to form a complete 3D shape. It is fairly easy with an equilateral triangle, which requires 4 sides, and for a square, with 6, but when I got to pentagons many problems arised.
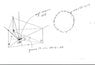
For one I was trying to calculate the angle the corners of 3 pentagons would have to be placed up agaisnt each other relative to a plane (see drawing). I ended up just assuming that the angle was 12, though I really have no idea, and continued with my estimates. So assuming that x (in the diagram) is 12 degrees, then I can calculate that the angle of each face to the other is about 156 degrees. With 156 I found the number of sides of a ploygon with those angles to be 15. From there I guesstimated that a pentagon forming a 3D shape by itself must have a minimum of around 80 faces.
Now I have several questions. Is my assumption that the angle x is 12, correct, if not how do I preform a correct calculation? Also what is the true number of sides a regular pentagon must have to form a 3D shape? Is there an equation which can identify the number of faces required for certain polygons to form 3d shapes? Finally, is there any way a single regular ploygon can approminate a sphere? Beyond a hexagon it is impossible to form 3D shapes since the measure of internal angles goes beyond 120, which means 3 corners cannot intersect.
Thanks,
-scott
Hopefully you can read this.
I have been thinking a lot recently about 3D shapes formed by 2D regular polygons. I was asking myself if there would be any way to calculate the minimium number of regular polygons to form a complete 3D shape. It is fairly easy with an equilateral triangle, which requires 4 sides, and for a square, with 6, but when I got to pentagons many problems arised.
For one I was trying to calculate the angle the corners of 3 pentagons would have to be placed up agaisnt each other relative to a plane (see drawing). I ended up just assuming that the angle was 12, though I really have no idea, and continued with my estimates. So assuming that x (in the diagram) is 12 degrees, then I can calculate that the angle of each face to the other is about 156 degrees. With 156 I found the number of sides of a ploygon with those angles to be 15. From there I guesstimated that a pentagon forming a 3D shape by itself must have a minimum of around 80 faces.
Now I have several questions. Is my assumption that the angle x is 12, correct, if not how do I preform a correct calculation? Also what is the true number of sides a regular pentagon must have to form a 3D shape? Is there an equation which can identify the number of faces required for certain polygons to form 3d shapes? Finally, is there any way a single regular ploygon can approminate a sphere? Beyond a hexagon it is impossible to form 3D shapes since the measure of internal angles goes beyond 120, which means 3 corners cannot intersect.
Thanks,
-scott
Hopefully you can read this.
Attachments
Last edited: