Change in Kinetic Energy

pcandrepair

1. The problem statement, all variables and given/known data

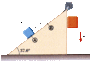
A m1 = 45.0 kg block and a m2 = 97.0 kg block are connected by a string as in the figure below. The pulley is frictionless and of negligible mass. The coefficient of kinetic friction between the 45.0 kg block and incline is 0.250. Determine the change in the kinetic energy of the 45.0 kg block as it moves from A to B, a distance of 20.0 m.

__________ J


2. Relevant equations

[tex]\Delta[/tex]E(mechanical) = [tex]\Sigma[/tex]W(non-conservative)

3. The attempt at a solution

First, I found the constant force of friction on m1:

(.25*m1*9.8*Cos37)

= 88.05N

Then I found the final velocity of the two system to be:

m2gd - friction force*d = 1/2(m1)Vf^2 + 1/2(m2)Vf^2

(97kg)(9.8m/s^2)(20m) - (88.05N)(20m) = 1/2(45)(Vf^2) + 1/2(97)(Vf^2)

17251 J = 1/2(45kg+97kg)(Vf^2)

Vf = sqrt((2*17251) / 142kg)

Vf = 15.5876 m/s

Then I used this velocity to find the change in kinetic energy of m1:

[tex]\Delta[/tex]K = Kf - Ki

= 1/2(m1)(Vf^2) - 1/2(m1)(Vf^2)

1/2(45kg)((15.5876m/s)^2) - 1/2(45kg)(0m/s)

[tex]\Delta[/tex]K = 5466.9 J

This answer sounds reasonable but I was wondering if someone could check my work. Any help would be appreciated.

Attached Thumbnails