MannyPacquiao
- 2
- 0
Homework Statement
Ok here it goes, we all know that 2 springs in series (k1, k2) can be expressed as one spring with spring constant k using the following equation.
<br /> k=\frac{1}{\frac{1}{k_{1}}+\frac{1}{k_{2}}}<br />
The same holds for 2 dampers c1 and c2.
<br /> c=\frac{1}{\frac{1}{c_{1}}+\frac{1}{c_{2}}}<br />
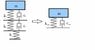
But what would happen if we have the system shown in the attached file. Point X is connected to S via a spring k1 and damper c1 in parallell, and point S is conncted to W via a spring k2 and damper c2 in parallell.
My question: If I'm only interested in points X and W, can the system be simplified into a one spring and one damper system?
Homework Equations
Already stated
The Attempt at a Solution
My initial guess is that the dynamics between X and W can be expressed with one spring and one damper with contants
<br /> k=\frac{1}{\frac{1}{k_{1}}+\frac{1}{k_{2}}}, c=\frac{1}{\frac{1}{c_{1}}+\frac{1}{c_{2}}}<br />
For this perticular question the masses are irrelevant, however in my original problem X and W have masses but S is massless.
Thanks in advance