jonwell
- 11
- 0
I was told this problem could be done with divergence theorem, instead of as a surface integral, by adding the unit disc on the bottom, doing the calculation, then subtracting it again.
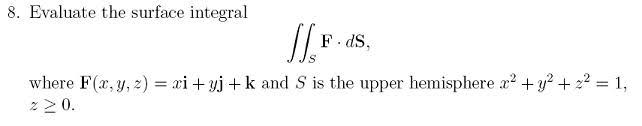
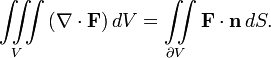
for del . f I get i + j = 2. Which makes the integral equal twice the volume of the hemisphere, or 4/3 pi. Now I'm supposed to subtract the unit disc, but I get pi when I calculate that surface, which leaves me with 1/3 pi. The answer should be 7/6 pi.
Thanks :)
Homework Statement
Homework Equations
The Attempt at a Solution
for del . f I get i + j = 2. Which makes the integral equal twice the volume of the hemisphere, or 4/3 pi. Now I'm supposed to subtract the unit disc, but I get pi when I calculate that surface, which leaves me with 1/3 pi. The answer should be 7/6 pi.
Thanks :)