Moment Inertia of a cube

Cosmossos

To which of the two cubes has a larger moment of inertia?

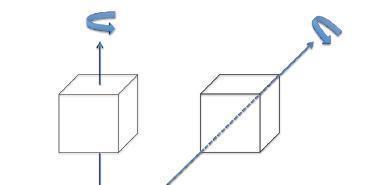
I think it's the right one, is it correct?
How can I explain that without using the parallel axis theorem?

berkeman

Why do you say the right one? Are you familiar with the relevant equation for calculating the moment of inertia?

Cosmossos

what relevant equation?

I think it's the right one because We know that the minimal moment of inertia is throw the principal axes that goes throw the center of mass. in the right one , the rotation isn't throw the principal axes . there is also the following theorem :

The moment of inertia about an arbitrary axis is equal to the
moment of inertia about a parallel axis passing through the
center of mass plus the moment of inertia of the body about
the arbitrary axis, taken as if all of the mass M of the body
were at the center of mass.

Am I wrong?

berkeman

There may be a shortcut way to tell which has a higher moment of inertia, but for me, I'd need to calculate it. I'd use the standard definition of the Mmoment of inertia, and evaluate thge integral for the diagonal case. I don't think you can use the parallel axis theorm, since the two axes are not parallel.

I'd do the 2-D case first, to see if it offered some intuition. That is, the moment of inertia for a flat rectangular sheet, with the axes going straight versus diagonal.

vela

I think they'll turn out to be equal. Try computing the moment of inertia tensor.