InvisibleMan1
- 40
- 0
To help me understand how a force is distributed over multiple connected objects, I have been trying to draw the FBDs of two stacked boxes which are sitting on the ground. I haven't been able to solve the problem however, and looking for the solution with Google did not turn up anything useful. I'm aware of Newton's third law, but I still have not been able to solve this... I'm at a loss, which is why I am posting here.
Here is an image of the problem:
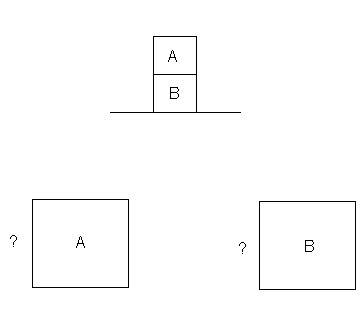
One attempt at solving it using Newton's third law ended up as (what appeared to be) an infinite loop of action-and-reaction forces going up and down the stack. I tried thinking of the two objects as a single object, but that just ended in guesswork without anything real concrete.
What would the FBD of A and the FBD of B look like, with all involved forces?
Here is an image of the problem:
One attempt at solving it using Newton's third law ended up as (what appeared to be) an infinite loop of action-and-reaction forces going up and down the stack. I tried thinking of the two objects as a single object, but that just ended in guesswork without anything real concrete.
What would the FBD of A and the FBD of B look like, with all involved forces?