How Does Ampere's Law Treat External Currents in Magnetic Field Calculations?

  • Thread starter Thread starter cupid.callin
  • Start date Start date
  • Tags Tags
    Ampere Law
AI Thread Summary
Ampere's Law states that the closed-loop integral of the magnetic field B over a curve is proportional to the net current enclosed by that loop. In the discussed scenarios, while one configuration has two wires, only the current from the wire within the integration loop affects the result, leading to the same magnetic field calculation in both cases. The external current does contribute to the magnetic field but does not affect the integral when it is not enclosed by the loop. The confusion arises from the assumption that all currents influence the calculation equally, whereas only the enclosed current matters for the integral. Understanding the distinction between enclosed and external currents is crucial for correctly applying Ampere's Law.
cupid.callin
Messages
1,130
Reaction score
1
In ampere circuital law, ∫B.dl = μo inet
i includes current "only passing through the loop "

also B is the net mag field at any point "all to any current anywhere"

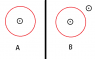
now look at the pic.

In A, it is very easy to find field using ampere law ... its μi/2πr

Also if in B is you apply the law, B is again μi/2πr ... how is this possible
its like the external current doesn't make any difference!

Plz explain me this !
 

Attachments

  • Untitled.png
    Untitled.png
    1.8 KB · Views: 429
Physics news on Phys.org
Ampere's law relies on what you define to be your curve of integration. Ampere's law states that the closed-loop integral Bdl over a given curve is proportional to the net current ENCLOSED by said loop.

In A you only have 1 wire enclosed by your curve of integration (red circle). In B, yes there are 2 wires, but only one is enclosed by your curve of integration, thus the same answer as in A.
 
Clever-Name said:
Ampere's law relies on what you define to be your curve of integration. Ampere's law states that the closed-loop integral Bdl over a given curve is proportional to the net current ENCLOSED by said loop.

In A you only have 1 wire enclosed by your curve of integration (red circle). In B, yes there are 2 wires, but only one is enclosed by your curve of integration, thus the same answer as in A.

So you are saying that i studied it wrong that in Bdl B is not due to all the currents existing in space?
 
cupid.callin said:
So you are saying that i studied it wrong that in Bdl B is not due to all the currents existing in space?
No, no, you are correct. B is due to the combined effect from all the currents.

cupid.callin said:
Also if in B is you apply the law, B is again μi/2πr ... how is this possible
its like the external current doesn't make any difference!
The integral \oint \vec{B} \cdot \vec{dl} gives the same result, but you cannot pull |\vec{B}| out like that because it is not constant in this case, unlike in the first!
 
Oh yes! you are right!

How can i ignore that thing !

Dumb of me !

Thanks a lot Fightfish !
 

Thread 'Rolling without slipping on a curved surface'

Kindly see the attached pdf. My attempt to solve it, is in it. I'm wondering if my solution is right. My idea is this: At any point of time, the ball may be assumed to be at an incline which is at an angle of θ(kindly see both the pics in the pdf file). The value of θ will continuously change and so will the value of friction. I'm not able to figure out, why my solution is wrong, if it is wrong .
View full post »
Thread 'Correct statement about a reservoir with an outlet pipe'

Thread 'Correct statement about a reservoir with an outlet pipe'

The answer to this question is statements (ii) and (iv) are correct. (i) This is FALSE because the speed of water in the tap is greater than speed at the water surface (ii) I don't even understand this statement. What does the "seal" part have to do with water flowing out? Won't the water still flow out through the tap until the tank is empty whether the reservoir is sealed or not? (iii) In my opinion, this statement would be correct. Increasing the gravitational potential energy of the...
View full post »
Thread 'A bead-mass oscillatory system problem'

Thread 'A bead-mass oscillatory system problem'

I can't figure out how to find the velocity of the particle at 37 degrees. Basically the bead moves with velocity towards right let's call it v1. The particle moves with some velocity v2. In frame of the bead, the particle is performing circular motion. So v of particle wrt bead would be perpendicular to the string. But how would I find the velocity of particle in ground frame? I tried using vectors to figure it out and the angle is coming out to be extremely long. One equation is by work...
View full post »

Similar threads

Finding magnetic field using Ampere's Circuital Law
Replies
5
Views
1K
Amperian loop-conceptual question
Replies
10
Views
3K
Magnetic energy density, self-inductance of coaxial cylindrical shells
Replies
10
Views
1K
Ampere's Law Problem: B-Field from a Current Distribution
Replies
6
Views
2K
Correct usage of Ampère's law for calculating B-field outside parallel wires?
Replies
4
Views
1K
Importance/Use of Gauss' Law and Ampere's Circuital Law
Replies
30
Views
2K
Rewriting the Ampere's law in term of free currents only
Replies
2
Views
1K
Magnitude of magnetic field at different points near a capacitor.
Replies
6
Views
969
Ampere's Law with a coaxial cable
Replies
2
Views
6K
How does an eddy current brake work exactly?
Replies
2
Views
2K

Hot Threads

Recent Insights

Back
Top