aero_zeppelin
- 85
- 0
Hi, I've been trying to nail this problem but I'm not sure if I'm stating it correctly:
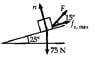
1. "A block weighing 75.0 N rests on a plane inclined at 25.0° to the horizontal. A force F is applied to the object at 40.0° to the horizontal, pushing it upward on the plane. The coefficients of static and kinetic friction between the block and the plane are, respectively, 0.363 and 0.156. (a) What is the minimum value of F that will prevent the block from slipping down the plane?"
Regarding the first question "a", this is what I have stated:
Ʃ Fx = Fsin15° + fs - (75 sin 25°) = 0
Ʃ Fy = n - ( 75 N cos 25°) + F cos 15° = 0
Having n= normal force , fs = static friction = (μs)(n) , μs = coefficient of static friction, and remembering the incline is the x-axis (using sin for it) and the y-axis perpendicular to it (using cos).
From ƩFy , we get n = ( 75 N cos 25°) - F cos 15°
Then from ƩFx, we get fs = (75 sin 25°) - Fsin15°
Considering fs = (μs)(n), we substitute and get:
(μs)(n) = (75 sin 25°) - Fsin15° and then we substitute n and get:
(μs) ( 75 N cos 25° - F cos 15°) = (75 sin 25°) - Fsin15°
Solving for F I get F = 40 N or something, but the book says it's F= 8.05 N.
Maybe I'm stating the sum of forces above wrong... Please help! Thx!
1. "A block weighing 75.0 N rests on a plane inclined at 25.0° to the horizontal. A force F is applied to the object at 40.0° to the horizontal, pushing it upward on the plane. The coefficients of static and kinetic friction between the block and the plane are, respectively, 0.363 and 0.156. (a) What is the minimum value of F that will prevent the block from slipping down the plane?"
Homework Equations
Regarding the first question "a", this is what I have stated:
Ʃ Fx = Fsin15° + fs - (75 sin 25°) = 0
Ʃ Fy = n - ( 75 N cos 25°) + F cos 15° = 0
Having n= normal force , fs = static friction = (μs)(n) , μs = coefficient of static friction, and remembering the incline is the x-axis (using sin for it) and the y-axis perpendicular to it (using cos).
The Attempt at a Solution
From ƩFy , we get n = ( 75 N cos 25°) - F cos 15°
Then from ƩFx, we get fs = (75 sin 25°) - Fsin15°
Considering fs = (μs)(n), we substitute and get:
(μs)(n) = (75 sin 25°) - Fsin15° and then we substitute n and get:
(μs) ( 75 N cos 25° - F cos 15°) = (75 sin 25°) - Fsin15°
Solving for F I get F = 40 N or something, but the book says it's F= 8.05 N.
Maybe I'm stating the sum of forces above wrong... Please help! Thx!