sandy.bridge
- 797
- 1
Homework Statement
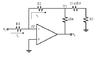
Here's the network:
R1=100
The gain ranges from -1V/V ---> -10V/V and the potentiometer R4=10.
Is R4 and R3 in parallel with each other? I can't seem to get the right answer...
Moreover, this is what was done:
-(R2/R1)(1+(R4/R2)+(R4/R3))=-10
Can someone please explain this. I know what the -10 means, I just do not really understand what was done here, whether it be a voltage divider, current divider or neither.
Regards, D.