peripatein
- 868
- 0
Homework Statement
When calculating the difference in pressure inside a spherical raindrop, the force exerted by the surface tension is calculated to be 2pi*R*gama, where R is the radius of the drop and gamma is dE/dS (dyne/cm).
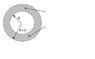
When the shape of the raindrop is said to be that of a torus, the force exerted by the surface tension is calculated to be 2pi*R*gamma + 2pi(R+2r)*gamma (please see attachment).
My question is simply why does the force in the case of the torus have two components, whereas in the case of a sphere it has only one?