Axial field from a pointed tip inside cylinder with flows

[Madoro]

Homework Statement

Hello, I have an experimental problem that I don´t know how to express theoretically.
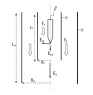
It consists on a tip at high voltage inside an earthed cylinder, where a discharge is produced. The discharge is radial, since is the shortest distance to the wall, and produces ions, which are dragged out by an air flow f₁, generating an electrical field in the axial direction E_x1 (fig. discharge.png).
There is an extra air flow f₂ that joins f₁ into a surrounding earthed cylinder, and then the field by the ions changes its value, E_x, since the flow is bigger and is further away from the discharge.

I have no clue neither how to calculate E_x1 nor E_x2. The attempt at a solution

I have tried to solve it supposing the discharge as a charged ring, similarly to how is done in this thread:
https://www.physicsforums.com/showthread.php?t=497126&highlight=radial+field+flow
Therefore, the electrical field at the output of the inner cylinder would be:
E_{x1}=\frac{q}{4\pi \epsilon_0}\frac{L_i}{(L_i^2+R_i^2)^{3/2}}

and therefore in the outer:
E_x=E_{x1}+\frac{q}{4\pi \epsilon_0}\frac{L_o}{(L_o^2+R_o^2)^{3/2}}

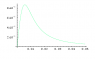
obtaining the solution shown in Ex.png.

First of all, is a good approximation the rings to the solution?
and secondly, why the axial field does this increase in the curve? should´t it be constantly decreasing?

Any help would be really appreciated, since I’m stuck here for long time now.
Thanks in advance.

 

[Madoro]

Second attempt:

I divide the problem in two parts, first inside the inner cylinder and then in the bigger one. I'll begin in the inner one where discharge is started
I suppose a radial discharge from the tip to the walls:
E_r=\frac{U}{r Log(R_i/R_{tip})}
being U the applied voltage and R_{tip} the radius of the needle's tip.

The governing equations (all in cylindrical coordinates) are the Poisson equation for the field inside the inner cylinder:
\frac{1}{r}\frac{\partial (r E_r)}{\partial r}+\frac{\partial E_z}{\partial z}=\frac{\rho}{\epsilon_0} (1)

and the convection-diffussion equation for the charge density:
\frac{\partial \rho}{\partial t}=D_i \nabla^2 \rho + \nabla \cdot (u \rho)=0 (2)

where D_i is the diffusion coefficient and is so small that this term can be neglected. Velocities in axial and radial directions are:
u_r=Z_i E_r
u_z=u_g+Z_i E_z
with u_g the f_1 flow velocity.

Therefore eq. (2):
\frac{1}{r}\frac{\partial (r Z_i E_r \rho)}{\partial r}+\frac{\partial ((u_g+ Z_i E_z) \rho))}{\partial z}=0 (2b)

Solving eq. (1) and (2b):

\frac{\partial E_z}{\partial z}=\frac{\rho}{\epsilon_0} (3)

Z_i E_r \frac{\partial \rho}{\partial r}+(u_g+ Z_i E_z) \frac{\partial \rho}{\partial z} + \rho Z_i \frac{\partial E_z}{\partial z}=0 (4)

Substituting eq. (3) into eq.(4):
Z_i E_r \frac{\partial \rho}{\partial r}+(u_g+ Z_i E_z) \frac{\partial \rho}{\partial z} + \frac{\rho^2 Z_i}{\epsilon_0}=0 (4b)


Therefore I have a system of 2 equations (3 & 4b) with 2 unknowns (E_z and \rho(z,r)), but I'm totally stuck on how to solve it.

Please, correct me if my approach of the problem is not correct or there is any mistake in the resolution. I could use some software to solve the system of equations, but I'm not sure if they are resoluble.

Thanks in advance.