Jeff12341234
- 179
- 0
I'm getting different answers for this integral

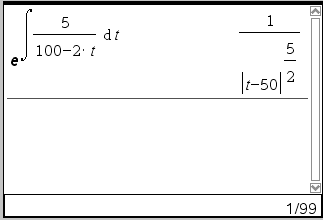
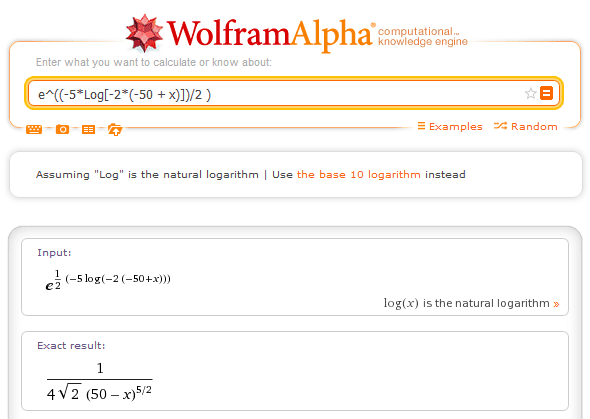
The forum discussion centers on discrepancies between the integral results produced by the TI-nSpire calculator and Wolfram Alpha (WA). Users assert that while both tools provide valid answers, they differ due to the handling of integration constants. The consensus is that indefinite integrals can yield multiple correct forms, depending on the chosen constants. The discussion emphasizes the importance of recognizing that calculators may not present the complete set of solutions, particularly when singularities are involved.
PREREQUISITESMathematics students, educators, and anyone using calculators for integral calculus who seeks to understand discrepancies in computational results.
Jeff12341234 said:There should only be one correct answer and several ways to write it. In this case, the answers are different, not just written differently. One is right, and the others are wrong. I'm trying to verify which one is truly correct.
Jeff12341234 said:There should only be one correct answer and several ways to write it. In this case, the answers are different, not just written differently. One is right, and the others are wrong. I'm trying to verify which one is truly correct.
Borek said:I have a hard time finding why you expect both TI and WA input to be equivalent.
bringing up the "+c" that gets added to any integration solution doesn't address the original question. It's unrelated. It doesn't in any way address the question of which of the 3 answers is right since the differences in the answers clearly don't have anything to do with the arbitrary constant.I like Serena said:Suppose we calculate:
$$e^{\int dt} = e^{t +C} = e^C e^t \qquad (1)$$
Both ##e^t## and ##2 e^t## are correct answers for (1).
You'll get the first if we pick C=0, and the second if we pick C=ln 2.
You might also say that the correct answer for (1) is:
$$e^{\int dt} = De^t$$
where D is an arbitrary integration constant.
It appears that your Ti-nSpire is not equipped to show integration constants.
Jeff12341234 said:bringing up the "+c" that gets added to any integration solution doesn't address the original question. It's unrelated. It doesn't in any way address the question of which of the 3 answers is right since the differences in the answers clearly don't have anything to do with the arbitrary constant.
To conclude, it appears that the image below is the correct answer + c. I don't know wtf wolfram alpha is doing..
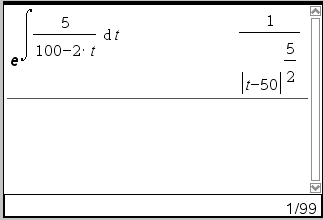
Ray Vickson said:No, thee "+c" issue is not unrelated---it is the crux of most of your problem. The fact is that Wolfram Alpha should have written |x-50| or |50-x| instead of 50-x, but that is the only thing "wrong" about its answer, and even that is not wrong if x < 50. Exactly WHY do you think the +C issue is irrelevant? Just saying it does not make it true; you need to *demonstrate* it.
micromass said:Hmm, I see: http://www.wolframalpha.com/input/?i=e^%28int+5%2F%28100+-+2t%29+dt+%29
Jeff12341234 said:now, +c wasn't added to the first part of this 2 step process. I just took the answer wolfram gave, set it as a power of e, and let wolfram simplify it. Even so, the answer in the first step is wrong/different from what I get from the Ti-nSpire. I get -5/2*ln(x-50)
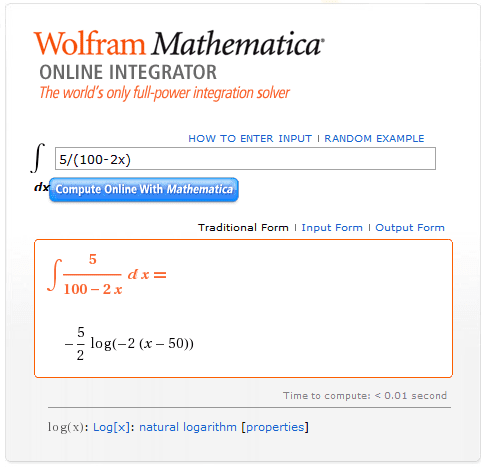
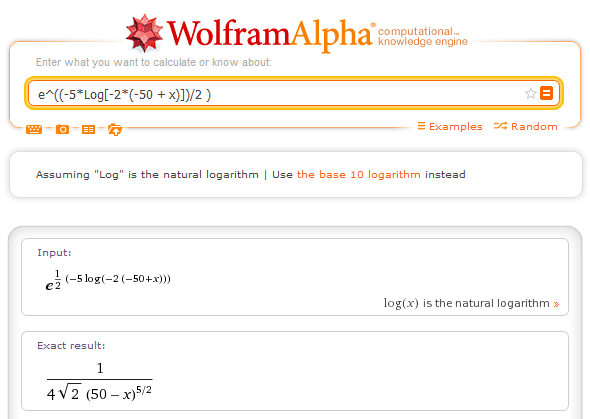
Jeff12341234 said:yep, that's essentially what I got from WA earlier. It's still different from the Ti's answer. As I've been saying since the beginning, they can't both be right.
Jeff12341234 said:The two different answers have different graphs though.
Am I to assume that either answer will give me the right result when using it during the process of solving a D.E.??
I like Serena said:Regardless what your Ti and W|A are saying (mathematically speaking they are both wrong), the proper calculation is:
micromass said:Well, strictly speaking, WA is not wrong. When wolfram alpha calculates an integral, it just gives one solution and it doesn't give the constant of integration.
micromass said:Well, strictly speaking, WA is not wrong. When wolfram alpha calculates an integral, it just gives one solution and it doesn't give the constant of integration.
Your solutions is of course correct, but it is equal for a correct choice of contants. (I wish to stress that WA allows the constants of integration to be complex!).
The trickery part in this problem is that the original function doesn't exist in the point t=50. This means that the constants of integration will not be unique. Like you did, you found constants D_1 and D_2.
But if you're just interested in one particular solution (like WA), then the answer of WA is perfectly valid.
I like Serena said:Btw, doesn't the solution to an indefinite integral require the integration constant?
Jeff12341234 said:If you take away D1 and/or D2, the equation matches with what the Ti spit out. Therefore, it seems that the Ti would be the answer to go with.