Stickybees
- 36
- 0
Does anyone know where this forumula comes from?
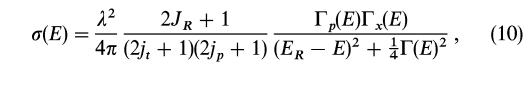
http://iopscience.iop.org/0067-0049/134/1/151/fulltext/
I don't quite understand the resonance widths, it's probably a naive question but what is 'resonating' in this context?
Thanks!
http://iopscience.iop.org/0067-0049/134/1/151/fulltext/
I don't quite understand the resonance widths, it's probably a naive question but what is 'resonating' in this context?
Thanks!