LagrangeEuler
- 711
- 22
Homework Statement
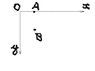
Particle goes to free fall from point ##A## to point ##B##. ##\upsilon_{A}=0##. How to define law of conservation of energy. Coordinate system is selected in such way that ##y## coordinate od point ##A## is zero. (See figure energy)
Homework Equations
For free fall ##\upsilon_{B}=\sqrt{2gy}##.
The Attempt at a Solution
My problem is with formulation of law of conservation of energy. Energy of point ##A## is in this case ##0##? Right? Because potential energy is zero (##y## cordinate of point ##A## is zero) and in case of free fall ##\upsilon_{A}=0##.
And energy of point ##B## is also zero ##-mgy+m\frac{\upsilon^2}{2}=0##.
Am I right? I'm confused how the energy of the particle could be zero? Can you help me? Give me some other view?