Charged particle moving under electric field

[utkarshakash]

Homework Statement

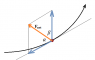
A charged particle having charge q and mass m is projected into a region of uniform electric field of strength E, with velocity v perpendicular to E. Throughout the motion apart from electric force particle also experiences a dissipative force of constant magnitude qE and directed opposite to its velocity. If |v|=6 m/s, then find its speed when it has turned through an angle of 90.

The Attempt at a Solution

The trajectory of the particle will be a curved path. Work done by dissipative force = ΔK.E.

qEx=\dfrac{1}{2} m(v_f ^2 - v^2)

But how do I find the path length traversed by the particle? It would be helpful if someone could guide me.

 

[TSny]

Let the x-axis be in the direction of the initial velocity and the y-axis in the direction of the field.

Draw a diagram showing the two forces acting on the particle at some point of the trajectory. Draw the net force on the diagram. Consider the acute angle that the net force makes to the tangent of the trajectory and consider the angle that the net force makes to the y-direction. How do those two angles compare?

What does that tell you about dv/dt and dv_y/dt, where v is the speed and v_y the y-component of velocity?

 

[utkarshakash]

Let the x-axis be in the direction of the initial velocity and the y-axis in the direction of the field.

Draw a diagram showing the two forces acting on the particle at some point of the trajectory. Draw the net force on the diagram. Consider the acute angle that the net force makes to the tangent of the trajectory and consider the angle that the net force makes to the y-direction. How do those two angles compare?

What does that tell you about dv/dt and dv_y/dt, where v is the speed and v_y the y-component of velocity?

I've got two equations

qE(1- \sin \theta ) = m \frac{dv_y}{dt} \\ -qE \cos \theta = m \frac{dv_x}{dt}

where θ is the angle made by the tangent with the +ve X-axis.

 

[TSny]

I've got two equations

qE(1- \sin \theta ) = m \frac{dv_y}{dt} \\ -qE \cos \theta = m \frac{dv_x}{dt}

where θ is the angle made by the tangent with the +ve X-axis.

OK, these equations look correct. But you can avoid having to deal with them if you continue along the lines that I suggested in my previous post.

From the vector diagram of the forces, can you see how the component of the net force along the tangent to the trajectory is related to the y-component of the net force?

 

[utkarshakash]

OK, these equations look correct. But you can avoid having to deal with them if you continue along the lines that I suggested in my previous post.

From the vector diagram of the forces, can you see how the component of the net force along the tangent to the trajectory is related to the y-component of the net force?

Magnitude of net force = 2qEcosα

Magnitude of component of net force along tangent = Magnitude of y-component of net force = 2qEcos²α

where α is the angle made by the net force with vertical.

 

[TSny]

Look at the two forces acting on the particle and the net force produced by these two forces. See the attached figure. Let $\small \alpha$ and $\small \beta$ be the angles between the net force and the tangential and y directions, respectively. From the fact that the two individual forces are equal in magnitude, what can you conclude about $\small \alpha$ and $\small \beta$?

 

[TSny]

Magnitude of component of net force along tangent = Magnitude of y-component of net force

OK, good. This is the key point.

So what is the relation between dv/dt and dv_y/dt?

 

[utkarshakash]

Look at the two forces acting on the particle and the net force produced by these two forces. See the attached figure. Let $\small \alpha$ and $\small \beta$ be the angles between the net force and the tangential and y directions, respectively. From the fact that the two individual forces are equal in magnitude, what can you conclude about $\small \alpha$ and $\small \beta$?

α=β

OK, good. This is the key point.

So what is the relation between dv/dt and dv_y/dt?

| \dfrac{dv}{dt} | = | \dfrac{dv_y}{dt} |

But where does this lead me?

 

[TSny]

α=β

| \dfrac{dv}{dt} | = | \dfrac{dv_y}{dt} |

But where does this lead me?

Noting the directions of the forces, what does this relation look like after you remove the absolute values?

Try integrating the relation.

 

[utkarshakash]

Noting the directions of the forces, what does this relation look like after you remove the absolute values?

Try integrating the relation.

v=v_y. Does this mean that the velocity of particle will be 6 m/s?

 

[TSny]

v=v_y. Does this mean that the velocity of particle will be 6 m/s?

You didn't get quite get the relationship correct. First decide if dv/dt = dv_y/dt or if dv/dt = -dv_y/dt. (Consider the directions of the components of the net force along the tangential and y directions.)

If two functions have the same derivative, it doesn't necessarily mean that the functions are equal. But what can you say about them?

 

[utkarshakash]

You didn't get quite get the relationship correct. First decide if dv/dt = dv_y/dt or if dv/dt = -dv_y/dt. (Consider the directions of the components of the net force along the tangential and y directions.)

If two functions have the same derivative, it doesn't necessarily mean that the functions are equal. But what can you say about them?

I think it should be dv/dt=dv_y/dt. From this I can only tell that their accelerations in two directions are equal.

 

[TSny]

If you look at the figure in post #6, you can see that the net force (red vector) projected onto the tangent line is in the direction to slow the particle down. But the net force has a positive y-component. So, v is decreasing while v_y is increasing. So, you need to write

dv/dt = -dv_y/dt.

Or

d(v+v_y)/dt = 0.

So, you have a quantity whose time derivative is zero. What can you conclude about that quantity?

 

[utkarshakash]

If you look at the figure in post #6, you can see that the net force (red vector) projected onto the tangent line is in the direction to slow the particle down. But the net force has a positive y-component. So, v is decreasing while v_y is increasing. So, you need to write

dv/dt = -dv_y/dt.

Or

d(v+v_y)/dt = 0.

So, you have a quantity whose time derivative is zero. What can you conclude about that quantity?

It must be constant. Initially, v+v_y=v=6(as v_y=0). When the particle turns through 90°, the particle only possesses vertical velocity. So, it must be 6, right?

 

[TSny]

It must be constant. Initially, v+v_y=v=6(as v_y=0).

That looks good. So, v + v_y = v₀ at all times.

When the particle turns through 90°, the particle only possesses vertical velocity. So, it must be 6, right?

When the particle has only vertical velocity, how does v compare with v_y?

 

[utkarshakash]

That looks good. So, v + v_y = v₀ at all times.



When the particle has only vertical velocity, how does v compare with v_y?

I guess they become equal to each other. Is it so?

 

[TSny]

I guess they become equal to each other. Is it so?

Yes. So, what is the final speed (after a 90^o turn)?

 

[utkarshakash]

Yes. So, what is the final speed (after a 90^o turn)?

3m/s. But I'm still not satisfied why they would become equal to each other.

 

[Vibhor]

I agree $\small \alpha = \small \beta$ .But I wonder how does that help us to deduce that $| \dfrac{dv}{dt} | = | \dfrac{dv_y}{dt} |$

I agree this is correct . I can derive it mathematically but not by looking at the diagram and from the fact that $\small \alpha = \small \beta$ .

$| \dfrac{dv}{dt} | ≠ qE$ .

Please help me understand how the equality of two angles lead us to $| \dfrac{dv}{dt} | = | \dfrac{dv_y}{dt} |$

 

[TSny]

3m/s. But I'm still not satisfied why they would become equal to each other.

$\small v = \sqrt{v_x^2+v_y^2}$. What is $\small v_x$ after a 90^o turn?

 

[utkarshakash]

$\small v = \sqrt{v_x^2+v_y^2}$. What is $\small v_x$ after a 90^o turn?

Nice. Thanks for having so much patience to guide me.

 

[TSny]

I agree $\small \alpha = \small \beta$

Please help me understand how the equality of two angles lead us to $| \dfrac{dv}{dt} | = | \dfrac{dv_y}{dt} |$

Using the figure in post #6, consider the projection of the net force onto the tangent line of the trajectory. Compare that with the projection of the net force onto the vertical (y) direction.

What does Newton's second law then tell you about the tangential- and y-components of acceleration: a_t and a_y?

How is tangential acceleration related to the rate of change of speed of the particle?

-------
Edit: Or you can use the figure attached here to see that the magnitude of the net force in the y-direction equals the magnitude of the net force along the tangent line.

 

[utkarshakash]

$\small v = \sqrt{v_x^2+v_y^2}$. What is $\small v_x$ after a 90^o turn?

Your method is absolutely brilliant. May I know how did it occur to you at first glance? (just curious )

 

[Vibhor]

I am just trying to get to the root of my confusion .

Am I right if I say $$ \dfrac{dv}{dt} ≠ qE $$ ?

 

[TSny]

May I know how did it occur to you at first glance?

It was not at first glance at all. I did not see the simple approach based on the diagram until after I had blindly proceeded to solve the same differential equations that you found in post #3:

qE(1- \sin \theta ) = m \frac{dv_y}{dt} \\ -qE \cos \theta = m \frac{dv_x}{dt}

Dividing these, you get $\large \frac{dv_x}{dv_y} = -\frac{\cos\theta}{1-\sin\theta}$

Using $v_x = v\cos\theta$ and $v_y = v\sin\theta$ you can get a differential equation for $\frac{dv}{d\theta}$ which can be integrated to get the solution

$\large v = \frac{v_0}{1+\sin\theta}$.

This simple result made me step back and look for a more direct way to get the answer. Somewhere in working with the equations, I had noticed $\frac{dv}{dt} = -\frac{dv_y}{dt}$ and that this was the key to a simple solution. Then I realized that this relation could easily be deduced from the force diagram.

So, it was a very circuitous route. I wish I could say that I had the insight to see the simple solution straightaway, but I didn't.

 

[TSny]

I am just trying to get to the root of my confusion .

Am I right if I say $$ \dfrac{dv}{dt} ≠ qE $$ ?

$\large \frac{dv}{dt}$ is the tangential acceleration. So, $\large \frac{dv}{dt} = \frac{F_{t}}{m}$ where $F_t$ is the net tangential force acting on the particle.

You can get the net tangential force from the diagram: $F_{t} = F\cos \phi - F = -qE(1-\cos\phi)$

 

[Vibhor]

Thanks for your patience .I am finding it difficult to express myself but I guess I am coming close .

Using the figure in post #6, consider the projection of the net force onto the tangent line of the trajectory. Compare that with the projection of the net force onto the vertical (y) direction..

The projections are equal . Are you trying to convey to me that the projection of the net force on the tangent line is dv/dt ?

I guess this is where I am stumbling .

 

[TSny]

Are you trying to convey to me that the projection of the net force on the tangent line is dv/dt ?

From Newton's second law applied to the tangential direction, the projection of the net force on the tangent line is $F_t = ma_t$ where $a_t$ is the tangential component of acceleration.

You can show that $a_t = \large \frac{dv}{dt}$, where $\small v$ is the speed of the particle.

One way to see that $a_t = \large \frac{dv}{dt}$, is to note that the velocity vector may be written $\vec{v} = v \; \hat{e_t}$, where $\hat{e_t}$ is a unit vector tangent to the trajectory. So, the acceleration vector is $$\vec{a} = \frac{d\vec{v}}{dt} = \frac{d(v\hat{e_t})}{dt}= \frac{dv}{dt}\hat{e_t} + v\frac{d\hat{e_t}}{dt}$$
But $\large \frac{d\hat{e_t}}{dt}$ is either zero or points in a direction perpendicular to $\hat{e_t}$. So, the first term on the right hand side of the equation above must be the tangential component of acceleration.

So, $a_t = \frac{dv}{dt}$

Then the projection of the net force on the tangent line is $F_t = ma_t = m\frac{dv}{dt}$.

 

[Vibhor]

The starting premise was that the net force was a resultant of two forces of equal magnitude . Force in y-direction = Force along the tangent =qE .From this we got $\small \alpha = \small \beta$ .Now when we project the net force along the tangent and along the y-axis ,we should get back the two original components of net force . In y-direction it is alright to say that the projection is qE .

But the projection of the net force along the tangent should also be qE and not dv/dt ?

Because dv/dt ≠ qE but is equal to qEcosθ – qE .

This is the issue I am having when you equate $| \dfrac{dv}{dt} | = | \dfrac{dv_y}{dt} |$ .Because $| \dfrac{dv}{dt} |$ is not the projection on the tangent .

Why this contradiction ? I guess I am not seeing something very obvious .

 

[TSny]

From the diagrams you should be able to see that the net force in the y-direction and the net force in the tangent direction have the same magnitude: $qE(1-\cos\phi)$.

The starting premise was that the net force was a resultant of two forces of equal magnitude . Force in y-direction = Force along the tangent =qE .From this we got $\small \alpha = \small \beta$ .Now when we project the net force along the tangent and along the y-axis ,we should get back the two original components of net force . In y-direction it is alright to say that the projection is qE .

It looks like you might be forgetting the red vectors in the diagrams when thinking about the net force in the y or tangent direction.

 

[Vibhor]

Your diagnosis is spot on :thumbs:

Thanks a ton