Saitama
- 4,244
- 93
Homework Statement
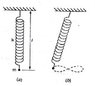
A mass ##m## on the end of a light spring of force constant ##k## stretches the spring to a length ##l## when at rest. The mass is now set into motion so it executes up and down vibrations while swinging back and forth as a pendulum. The mass moves in a figure-eight pattern in a vertical plane, as shown in the figure. Find the force constant in terms of ##m##,##l## and ##g##.
(Ans: k=4mg/l )
Homework Equations
The Attempt at a Solution
I noticed that the curve traced by the hanging mass is of the form ##r^2=a\cos(2\theta)## with the mass ##m## being at the origin at ##t=0##. But I don't think this is going to help. This is a question from one of my practice sheets and I doubt I need to deal with polar curves which aren't generally taught in high school.
How do I approach this problem?
Any help is appreciated. Thanks!
Attachments
Last edited: