Bound Definition and 475 Threads
-
B
MHB An approximated lower bound of an expression.
Hii All, $ \sum_{i=1}^{x}i^{N}:N>2 $. Is there any approximated lower bound for the above summation? Is it > $ \frac{1}{N+1}x^{(N+1)}$ ? If yes, how to prove that?regards, Bincy -
M
Graduate How to Estimate the Operator Norm ||A||_2 for a Difference Operator?
Greetings everyone! I have a set of tasks I need to solve using using operator norms, inner product... and have some problems with the task in the attachment. I would really appreciate your help and advice. This is what I have been thinking about so far: I have to calculate a non trivial upper...- Max Fleiss
- Thread
- Bound Norm Operator Upper bound
- Replies: 1
- Forum: Topology and Analysis
-
H
Graduate Excitons: Opposite Movements of Bound Electron-Hole Pairs
How a bound electron-hole pair (exciton) can move together while the velocity of the free electron in the conduction band is opposite to that of the corresponding hole in the valence band?- hokhani
- Thread
- Bound
- Replies: 7
- Forum: Atomic and Condensed Matter
-

Variable Magnetic field bound in a cylindrical region
Homework Statement There is a uniform but variable magnetic field ##\vec{B}=(B_0 t)(-\hat{k})##, in a cylindrical region, whose boundary is described by ##x^2+y^2=a^2##. ##\displaystyle \int_P^{Q} \vec{E} \cdot \vec{dy}## is (see attachment 1) A)0 B)##\frac{\pi}{4}(B_0 a^2)##...- Saitama
- Thread
- Bound Cylindrical Field Magnetic Magnetic field Variable
- Replies: 9
- Forum: Introductory Physics Homework Help
-
7
Graduate Energies and numbers of bound states in finite potential well
Hello I understand how to approach finite potential well. However i am disturbed by equation which describes number of states ##N## for a finite potential well (##d## is a width of a well and ##W_p## is potential): $$ N \approx \dfrac{\sqrt{2m W_p}d}{\hbar \pi} $$ I am sure it has something to...- 71GA
- Thread
- Bound Bound states Energies Finite Numbers Potential Potential well States
- Replies: 2
- Forum: Quantum Physics
-
A
Graduate Brownian Particle bound by a Spring / internal Energy
Hi, i regard a Brownian Particle connectet to a Spring and there is a heat-reservoir. The distribution of the x-coordinate of the particle follows the Diffusion-Equation (Fokker-Planck-Equation): \partial_{t}P(x,t)=\frac{D}{2} \partial_{x}^{2}P(x,t)- \Gamma\partial_{x}[f(x)P(x,t)] A... -
M
Undergrad Lower and Upper bound proof in R
I am getting lost in the proof in the 5th line when it says there are 10 numbers that have the same kth digit as x. Why 10? I don't understand where this number is coming from and it doesn't seem arbitrary. the rest of the proof...- MotoPayton
- Thread
- Bound Proof Upper bound
- Replies: 1
- Forum: Set Theory, Logic, Probability, Statistics
-

Graduate What is the maximum entropy a system can have based on its energy and size?
ok so my main question here is about the normal bekenstein bound, but I will go into why I'm asking too in case anyone has any comments on that. The way I understand the derivation of the bekenstein bound is: If you have some closed system with energy E bounded by radius R, you can derive the...- michael879
- Thread
- Bound
- Replies: 39
- Forum: Special and General Relativity
-
H
Graduate Help with Problem on Bekenstein Bound
Hi Guys, I've been struggling over a problem with the Bekenstein Bound, and I wonder if someone can help, please. The Bekenstein Bound is derived from the entropy of black holes, and says that the maximum information content of a region of space is proportional the area of that region, not...- HowardTheDuck
- Thread
- Bound
- Replies: 16
- Forum: Special and General Relativity
-
O
MHB Least upper bound - greatest lower bound duality
Hello everyone! There's a point I didn't get in Rudin's theorem 1.11 that says: Suppose S is an ordered set with the LUB property, and B $\subset$ S, B is not empty and B is bounded below. Let L be the set of lower bounds of B. Then a = sup L exists in S, and a - inf B. In particular inf B...- OhMyMarkov
- Thread
- Bound Duality Upper bound
- Replies: 1
- Forum: Topology and Analysis
-
M
Graduate Production of bound states of slow fermions- Peskin 5.3
Hi all, I've been reading section 5.3 of Peskin and Schroeder, in which the authors discuss the production of a bound state of a muon-antimuon pair close to threshold in electron-positron collisions. Here \xi,\xi' are the Weyl spinors used to construct the Dirac spinors for the muon and...- muppet
- Thread
- Bound Bound states Fermions Peskin States
- Replies: 3
- Forum: Quantum Physics
-
N
Doubt regarding derivation of bound charges in dielectric
In Griffiths, for deriving the bound charges for a given polarization P , the formula used is the general formula for dipoles .i.e ( equation 4.9) {Here the potential at r is calculated due to the dipole at r' ) V(r) = ∫\frac{x.P(r')}{X^2}d\tau' Here X = r - r' , and x = unit vector in...- nuclear_dog
- Thread
- Bound Charges Derivation Dielectric Doubt
- Replies: 2
- Forum: Introductory Physics Homework Help
-
H
Positive lower bound in the punctured rectangle
Homework Statement Let p(x,y) be a positive polynomial of degree n ,p(x,y)=0 only at the origin.Is it possible that the quotient p(x,y)/[absolute value(x)+absval(y)]^n will have a positive lower bound in the punctured rectangle [-1,1]x[-1,1]-{(0,0)}? Homework Equations The...- hedipaldi
- Thread
- Bound
- Replies: 7
- Forum: Calculus and Beyond Homework Help
-
P
Bound State Wavefunctions vs Non-Bound State Wavefunctions
Bound vs "not"bound states Homework Statement Hi, I do not understand how two bound state wavefunctions differ from not bound state wavefunctions. To be more precise I m thinking about the graphical representation. [b]ons[/b2. Relevant equati The Attempt at a Solution I speculate that bound...- prehisto
- Thread
- Bound Bound states States
- Replies: 1
- Forum: Advanced Physics Homework Help
-
A
Graduate Analytic continuation to find scattering bound states
Hello, I am trying to understand the idea of using analytic continuation to find bound states in a scattering problem. What do the poles of the reflection coefficient have to do with bound states? In a problem that my quantum professor did in class (from a previous final), we looked at the 1D...- alexvas
- Thread
- Analytic continuation Bound Bound states Scattering States
- Replies: 2
- Forum: Quantum Physics
-
S
What is the Lower Bound of this Sequence?
Homework Statement Homework Equations The Attempt at a Solution This is what I have so far: x_{n+1}=\frac{x^5_n + 1}{5x_n}=1 x_{n+2}=\frac{x^5_{n+1} + 1}{5x_{n+1}}=\frac{1^5+1}{5} I think you have to do some sort of repeated substitution but I don't quite see it. Any help? Thanks.- sunnybrooke
- Thread
- Bound Sequence
- Replies: 9
- Forum: Precalculus Mathematics Homework Help
-

Minimum energy of electron bound in nucleus
Homework Statement An electron is confined to a nucleus of radius 4 femtometres. Estimate its minimum energy. Homework Equations ΔxΔp_x=h/4\pi E^2=p^2c^2 + m^2c^4 As the electron's rest energy will be much less than it's kinetic energy, E=pc The Attempt at a Solution So I...- phosgene
- Thread
- Bound Electron Energy Minimum Nucleus
- Replies: 1
- Forum: Introductory Physics Homework Help
-
8
Graduate IS it possible to have total bound current NOT equal to 0?
I have a permanent magnetization \vec{M}=(ks)\hat{z}, k is just a const, s is the cylindrical coor. Then it turns out that the total bound current not equal to 0. i wonder is it possible? the magnetization is stored inside the shell of a cylinder of inner radius a and outer radius b. thanks in...- 8987846
- Thread
- Bound Current
- Replies: 1
- Forum: Electromagnetism
-
M
How to Prove an Upper Bound for a Set of Real Numbers?
Homework Statement Let A be a set of real numbers. If b is the supremum (least upper bound) of the set A then whenever c<b there exist an a in A such that a>c. Homework Equations The Attempt at a Solution I considered two cases. The first one when the supremum b is attained by...- matematiker
- Thread
- Bound Proof Set Upper bound
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
T
Undergrad Understanding Free & Bound Charges: H & D Fields Explained
My teacher's notes don't explain this. What are free and bound charges, and why are the H and D field defined like they are?- Tosh5457
- Thread
- Bound Charges Fields
- Replies: 17
- Forum: Electromagnetism
-
R
Index out of bound because numel(w)=11
Hello,, I try to convert a fortran program to matlab. I want to make an absorbing boundary model. But when I run it, I keep getting an error says: ? Attempted to access w(12); index out of bounds because numel(w)=11. Error in ==> absorb_bound_coba at 45...- ria91
- Thread
- Bound Index
- Replies: 2
- Forum: MATLAB, Maple, Mathematica, LaTeX
-
G
Graduate Bound states in propagator
Why must it be true that a system that has a bound state must have its scattering amplitude have a pole in the upper half of the complex wave-number plane? For example, if the scattering amplitude as a function of the initial wave number magnitude |k| is: A=\frac{1}{|k|-iB} with B>0, then...- geoduck
- Thread
- Bound Bound states Propagator States
- Replies: 1
- Forum: Quantum Physics
-

Graduate Number of bound states and index theorems in quantum mechanics?
Just an idea: is there an index theorem for an n-dimensional Hamiltonian H = -\triangle^{(n)} + V(x) which "counts" the bound states (H - E) \,u_E(x) = 0 i.e. eigenfunctions and eigenvalues in the discrete spectrum of H?- tom.stoer
- Thread
- Bound Bound states In quantum mechanics Index Mechanics Quantum Quantum mechanics States
- Replies: 7
- Forum: Quantum Physics
-
E
Greatest lower bound problem - Rudin POMA Ch1 Exercise 5
Homework Statement 5. Let ##A## be a nonempty set of real numbers which is bounded below. Let ##-A## be the set of all numbers ##-x##, where ##x\in A##.Prove that $$\inf A=-\sup(-A)\text{.}$$ Homework Equations The Attempt at a Solution Does the proof below look OK? I am a bit uneasy...- EdMel
- Thread
- Bound Exercise
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
R
Difference Between Bound and Free charge
Homework Statement So I'm having a bit of trouble getting my head around this concept and was hoping someone would be able to shed some light on it. I know the definition. i.e free charge isn't bound to a nucleus whereas bound is. But physically what difference does this make. i.e are free...- rshalloo
- Thread
- Bound Charge Difference
- Replies: 1
- Forum: Introductory Physics Homework Help
-
B
Undergrad Least upper bound of open interval.
I am having trouble understanding how there could be a least upper bound for an open interval. If I have (a,b) and i am looking for the least upper bound X which is the number that is less than or equal to the set of Y such that Y> all the numbers in the interval (a,b) when I think about it I...- BareFootKing
- Thread
- Bound Interval Upper bound
- Replies: 2
- Forum: Set Theory, Logic, Probability, Statistics
-
D
Graduate Clarifications on the least upper bound property and the irrational numbers
Hello everyone. I desperately need clarifications on the least upper bound property (as the title suggests). Here's the main question: Why doesn't the set of rational numbers ℚ satisfy the least upper bound property? Every textbook/website answer I have found uses this example: Let...- drobadur
- Thread
- Bound Irrational Irrational numbers Numbers Property Upper bound
- Replies: 3
- Forum: Topology and Analysis
-
A
Graduate Bound charge in linear dielectric
How can we show that the bound charge in a homogeneous linear dielectric is proportional to the density of the free charge. I have a handful of equations but still I can't work this out.- amankr
- Thread
- Bound Charge Dielectric Linear
- Replies: 1
- Forum: Electromagnetism
-
B
Undergrad Why Do We Have Different Terms for Least Upper Bound and Supremum?
Are the least upper bound and supremum of a ordered field same thing? If so, then why do we have two different terms and why do textbooks do not use them interchangeably. That also means that greatest lower bound and infimum are also the same thing.- back2square1
- Thread
- Bound Supremum Upper bound
- Replies: 3
- Forum: Topology and Analysis
-
H
MHB How Accurate is Lagrange Interpolation for Approximating Cos(0.75)?
[FONT=Cambria]Problem: [FONT=Cambria]Use the Lagrange interpolating polynomial of degree three or less and four digit chopping arithmetic to approximate [FONT=times new roman]cos(.750) using the following values. Find an error bound for the approximation. [FONT=times new roman]cos(.6980) =... -
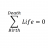
Upper Bound Proof of Sup(SUT)=max{sup(S), sup(T)}
Homework Statement Prove or disapprove, for non-empty, bounded sets S and T in ℝ : sup(SUT) = max{sup(S), sup(T)} Homework Equations The least upper bound axiom of course. The Attempt at a Solution Since we know S and T are non-empty and bounded in the reals, each of them...- STEMucator
- Thread
- Bound Proof Upper bound
- Replies: 11
- Forum: Calculus and Beyond Homework Help
-
C
Graduate Defining an upper/lower bound in lexicographically ordered C.
If I have a lexicographic ordering on ℂ, and I define a subset, A = \{z \in ℂ: z = a+bi; a,b \in ℝ, a<0\}. I have an upper bound, say α = 0+di. My question is does only the real part, Re(α) = 0 define the upper bound? Or does the Im(α) = d have nothing to do with bounds in general? Since it...- c0dy
- Thread
- Bound
- Replies: 1
- Forum: Topology and Analysis
-
U
Real Analysis Least Upper Bound Question
Homework Statement If S1, S2 are nonempty subsets of ℝ that are bounded from above, prove that l.u.b. {x+y : x \in S1, y \in S2 } = l.u.b. S1 + l.u.b. S2 Homework Equations Least Upper Bound Property The Attempt at a Solution Using the least upper bound property, let us suppose...- utstatistics
- Thread
- Analysis Bound Real analysis Upper bound
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-

Graduate Effect of cosmological expansion on bound systems in realistic cosmologies
This paper dates to 1998: Cooperstock, Faraoni, and Vollick, "The influence of the cosmological expansion on local systems," http://arxiv.org/abs/astro-ph/9803097v1 They show that systems such as the solar system, galaxies, and clusters of galaxies experience nonzero effects from cosmological...- bcrowell
- Thread
- Bound Cosmological Cosmological expansion Expansion Systems
- Replies: 18
- Forum: Special and General Relativity
-
V
Graduate What Happens When an Electron Enters an Infinite Square Well?
I have a question, and I'm positive it has a really simple answer, but I can't think of it right now. In the infinite square well (the simplest bound problem), the wave functions have discrete energy values. We can have a wave function that's a linear superposition of any number of these so...- VortexLattice
- Thread
- Bound Electron Stupid
- Replies: 4
- Forum: Quantum Physics
-
M
Definite Integration with Upper bound as another integral
i have a similar one. f(x) = \int\frac{dt}{\sqrt{1+t^3}} on (0, g(x)) g(x) = \int(1+sin(t^2))dt on (0, cos(x)) that is, these are definite integrals on the interval from zero up to the given function. the question is to solve f'(pi/2). the correct answer is -1 but i don't understand...- marathon
- Thread
- Bound Integral Integration Upper bound
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-

Graduate Lower Bound on Q(x) for X ~ Gaussian RV
I think everyone knows that Q(x)= P(X>x) where X is a Gaussian Random variable. Now I was reading about it and it says that Q(x) is bounded as follows Q(x)≤ (1/2)(e-x2/2) for x≥0 and Q(x)< [1/(√(2∏)x)](e-x2/2) for x≥0 and the lower bound is Q(x)> [1/(√(2∏)x)](1-1/x2) e-x2/2 for x≥0 Can...- iVenky
- Thread
- Bound Gaussian
- Replies: 1
- Forum: Set Theory, Logic, Probability, Statistics
-
R
Undergrad The least upper bound property and the irrationals.
Hi Does anybody know if the irrational numbers have the least upper bound property?- RediJedeye
- Thread
- Bound Property Upper bound
- Replies: 3
- Forum: Topology and Analysis
-

MHB What is the definition of greatest/least upper bound in a partially ordered set?
Let $a$, $b$ and $c$ be elements of a partially ordered set $P$. My book defines $c$ as the greatest upper bound of $a$ and $b$ if, for each $x \in L$, we have $x \le c$ if and only if $x \le a$ and $x \le b$. Similarly, it defines $c$ as the least upper bound of $a$ and $b$ if, for each $x \in...- QuestForInsight
- Thread
- Bound Upper bound
- Replies: 2
- Forum: Set Theory, Logic, Probability, Statistics
-
B
Graduate DE: Lower Bound for radius of convergence
Prb:(x^4+4*x^2+16)y"+4(x-1)y'+6xy=0 P=(x^4+4*x^2+16) Q=4(x-1) R=6x P=0 for - 1 - 3^(1/2)*i 1 - 3^(1/2)*i - 1 + 3^(1/2)*i 1 + 3^(1/2)*i Q=0 for 1 R=0 for 0 Do we ignore Q & R, plotting P, then find shortest distance which would equal 2?- BobMarly
- Thread
- Bound Convergence Radius Radius of convergence
- Replies: 1
- Forum: Differential Equations
-
Graduate Are Standard-Model particles bound states?
So far, we've discovered this compositeness hierarchy: Atoms - bound states of electrons, nuclei, photons Nuclei - bound states of nucleons and other hadrons Hadrons - bound states of quarks and gluons So are any Standard-Model particles bound states of any other particles? The...- lpetrich
- Thread
- Bound Bound states Particles States
- Replies: 2
- Forum: High Energy, Nuclear, Particle Physics
-
J
Graduate Need help finding a bound for an equation
I'm trying to find a value K>o such that for real a,b,c,d (a^2+c^2)x^2+2(ab+cd)xy+(b^2+d^2)y^2 ≤ K(x^2+y^2). Any help on this would be greatly appreciated thanks.- jacksonjs20
- Thread
- Bound
- Replies: 2
- Forum: Calculus
-
A
Graduate Could dark matter be invisible bound states of ordinary matter or ehm, aliens?
I've thought about dark matter and I'm wondering if it could possible be made up invisible bouond states of ordinary matter? Wikipedia says "According to consensus among cosmologists, dark matter is composed primarily of a new, not yet characterized, type of subatomic particle." But why a...- Antti
- Thread
- Aliens Bound Bound states Dark matter Invisible Matter States
- Replies: 1
- Forum: Astronomy and Astrophysics
-
B
Find the wave function of a particle bound in a semi-infinite square well
Homework Statement Consider the semi-infinite square well given by V(x) = -V0 < 0 for 0≤ x ≤ a and V(x) = 0 for x > a. There is an infinite barrier at x = 0 (hence the name "semi-infinite"). A particle with mass m is in a bound state in this potential with energy E ≤ 0. Solve the Schrödinger...- BPMead
- Thread
- Bound Function Particle Square Square well Wave Wave function
- Replies: 9
- Forum: Advanced Physics Homework Help
-
T
Proving Continuity of f(x,y) = y/(1+x2) Using Delta-Epsilon Bound
Use the delta-epsilon definition to prove f(x,y) = y/(1+x2) is continuous at (0,0)Attempts:So I'm doing some work and my main issue is finding a bound for the denominator of 1+x2: So work wise I have something looking like: \delta/(|1| + |x2| ). How could I found a good bound?- trap101
- Thread
- Bound Delta Epsilon
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
B
MHB Finding an Upper Bound for ln(x) in [0,1]
Hii everyone, Can anyone tell me a decent upper bound of Ln[x](which can mimic Ln[x]) where x is in [0,1]regards, Bincy -
N
Graduate Higher Bound State: Definition & Meaning
"higher" bound state just a quick question on terminology.. if something has a higher binding energy, can it be said to be in a higher bound state? thanks- njl86
- Thread
- Bound Bound state State
- Replies: 2
- Forum: Quantum Physics
-
N
Graduate Is the Bound State Wave Function Always Real or Imaginary?
Hi :), recently I was thinking whether every bound state is only real or imaginary, not mixture? Since all bound states have degeneracy of level one, if we suppose that ψ=ψ_{r}+iψ_{i}, then ψ_{r} and ψ_{i} must be linearly dependent as in opposite case there would be a bound state with...- Nemanja989
- Thread
- Bound Bound state Function State Wave Wave function
- Replies: 1
- Forum: Quantum Physics
-
A
Bound charges - are they real or mathematical?
In my chapter about electric fields in matter my book derives and expression for the potential due to the polarization of a dielectric material. For that you find that the polarization is equal to the potential of a collection of negative charges on the surface and positive charges inside the...- aaaa202
- Thread
- Bound Charges Mathematical
- Replies: 1
- Forum: Advanced Physics Homework Help
-
A
Understanding Bound Charges and Their Mathematical Derivation
Upon reading about bound charges I stumbled on something I didn't quite understand. It is not a physical thing but purely a mathematical thing. In the attached section my book wants to take the gradient: ∇'(1/r) with respect to the source coordinates, r'. Now, can someone by inspection...- aaaa202
- Thread
- Bound Charges Derivation
- Replies: 3
- Forum: Calculus and Beyond Homework Help