Exponent Definition and 212 Threads
-
L
Help calculating this limit please
Hi, I have problems with task b, more precisely with the calculation of the limit value: By the way, I got the following for task a ##f^{(n)}(x)=(-1)^{n+1} \frac{(n-1)}{x^n}## Unfortunately, I have no idea how to calculate the limit value for the remainder element, since ##n## appears in...- Lambda96
- Thread
- Calculation Exponent Limit
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
K
Undergrad Derivation for the indicial exponent in the Frobenius method
I'm reading a book called Asymptotic Methods and Perturbation Theory, and I came across a derivation that I just couldn't follow. Maybe its simple and I am missing something. Equation 3.3.3b below. y(x) takes the form A(x)*(x-x0)^α and A(x) is expanded in a taylor series.- Kloo
- Thread
- Derivation Exponent Frobenius Method
- Replies: 1
- Forum: Differential Equations
-

Graduate Does the Maximum Lyapunov exponent depend on the eigenvalues?
I am currently reading this paper where on page 8, the authors say that: This correlates with Figure 8 on page 12. Does it mean that there is a real correlation between eigenvalues and Lyapunov exponents?- codebpr
- Thread
- Chaos theory Correlation Eigen values Eigenvalues Exponent Lyapunov Maximum String theory
- Replies: 1
- Forum: Beyond the Standard Models
-

Evaluating several powers of ##x## from a given equation
[FONT=times new roman]Problem statement : If ##\boldsymbol{\displaystyle x^{\displaystyle 2x^{\displaystyle 6}}=3}##, evaluate ##\boldsymbol{\left(x^{\displaystyle x^{\displaystyle x^{\displaystyle 6}}}\right)^{\displaystyle\sqrt 3} = ?}##. Attempt : I copy and paste my attempt using Autodesk...- brotherbobby
- Thread
- Exponent Index
- Replies: 6
- Forum: Precalculus Mathematics Homework Help
-
Undergrad Algebra equation with variable as exponent
This equation takes a present value (PV) to find mortgage payments, PMT: Alternatively, switching V for PV and T for PMT: V/T = r(1-r^n)/(1-r) What is an algebraic method to solve for "r"? Can it not be solved for? I realize I can just find out "r" by trial by error in Excel using the PMT...- adamaero
- Thread
- Algebra Exponent Finance Variable
- Replies: 7
- Forum: Linear and Abstract Algebra
-
D
High School Can we have a complex number in the exponent?
Does it make sense to write ##r^c## where ## r\in R/e ## and ##c\in C## ?- docnet
- Thread
- Complex Complex number Exponent
- Replies: 2
- Forum: Topology and Analysis
-

MHB Can Exponent Values Be Determined with One Equation and Two Variables?
ok without any calculation I felt it could not be determined since we have one equation with 2 variables- karush
- Thread
- Exponent
- Replies: 4
- Forum: General Math
-
L
Cost Estimation capacity exponent formula
To estimate the cost of an item of equipment or plant from another of a known cost and size or capacity , we use a well known formula Cost B = Cost A * ( CapacityB/Capacity A)^n, where n is a factor usually around 0.5-0.8 depending on the plant or equipment involved. These exponents are...- LT Judd
- Thread
- Capacity Estimation Exponent Formula
- Replies: 4
- Forum: Materials and Chemical Engineering
-
P
Finding the efficiency of an ideal gas with adiabatic exponent 'γ'
Here is what I did : work done in going from A to C, W1 = 2nRToln(2) (isothermal process) work done in going from C to B, W1 = pΔV = nRΔT = -nRTo (isobaric process) work done in going from B to A, W3 = 0 (isochoric process) so, total work done = W1 + W2 + W3...- PhysicsEnthusiast123
- Thread
- Adiabatic Efficiency Exponent Gas Homework Ideal gas Thermodynamcics
- Replies: 3
- Forum: Introductory Physics Homework Help
-

MHB Unsolved Challenge: Natural logarithm and Exponent
Prove $e^{-x}\le \ln(e^x-x-\ln x)$ for $x>0$. -

MHB Factorials and Exponent Challenge
Find all positive integer solutions $(a,\,b,\,c,\,n)$ of the equation $2^n=a!+b!+c!$.- anemone
- Thread
- Challenge Exponent Factorials
- Replies: 2
- Forum: General Math
-
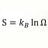
High School Obtaining a Future Numbers Increase With Exponent From Past Increase
Suppose on day-one a number is 15 then on day-twenty the number has increased to 200. Now I want to find out what that increasing number could be on day-forty by using the exponent derived from the day- one to day-twenty increase ; x(log15) = log 200 . x = 2.301/1.176 = 1.956. So now on day...- morrobay
- Thread
- Exponent Future increase Numbers
- Replies: 8
- Forum: Set Theory, Logic, Probability, Statistics
-

Undergrad Tetration except each repeated exponent increases by 1
I was just wondering what the proper notation would be to describe an infinite power tower which has each repeated exponent increasing by a value of 1, like such; $$a^{{{{{{(a+1)}^{(a+2)}}^{(a+3)}}^{.}}^{.}}^{.}}$$- Saracen Rue
- Thread
- Exponent
- Replies: 1
- Forum: Calculus
-
I
Expectation value of an angular momentum with a complex exponent
I am struggling to figure out how to calculate the expectation value because I am finding it hard to do something with the exponential. I tried using Euler's formula and some commutator relations, but I am always left with some term like ##\exp(L_z)## that I am not sure how to get rid of.- isochore
- Thread
- Angular Angular momentum Complex Expectation Expectation value Exponent Momentum Value
- Replies: 3
- Forum: Advanced Physics Homework Help
-

Undergrad Missing exponent in "Theoretical Minimum"?
In "The Theoretical Minimum" (the one on classical mechanics), on page 218, the authors write a Lagrangian $$L=\frac m 2 (\dot r^2 +r^2\dot \theta ^2)+\frac {GMm} r$$ They then apply the Euler-Lagrange equation ##\frac d {dt}\frac {dL} {d\dot r}=\frac {dL} {dr}## (I know there should be...- SamRoss
- Thread
- Error Exponent Lagrangian Minimum Mistake Theoretical Theoretical minimum
- Replies: 4
- Forum: Beyond the Standard Models
-
V
How to find the value of a complex number with high exponent
Homework Statement Find the value of (-√3 + i)43/243 Homework EquationsThe Attempt at a Solution I do not know how to really go about this problem. I know that i0=1, i1=i, i2=-1, i3=-i, and I tried to use that to help but I got to no where, I also tried to break up the exponent into...- ver_mathstats
- Thread
- Complex Complex number Exponent Value
- Replies: 10
- Forum: Calculus and Beyond Homework Help
-

High School 1 to the power of infinity, why is it indeterminate?
I've been taught that $$1^\infty$$ is undetermined case. Why is it so? Isn't $$1*1*1...=1$$ whatever times you would multiply it? So if you take a limit, say $$\lim_{n\to\infty} 1^n$$, doesn't it converge to 1? So why would the limit not exist?- navneet9431
- Thread
- Exponent Infinite Infinity Limits Power
- Replies: 20
- Forum: Calculus
-

High School Base e to an imaginary exponent seeming contradiction
<Moderator's note: Moved from a homework forum.> 1. Homework Statement Given 0 < a < 1, i = √(-1), ei2πa = cos 2πa + i sin 2πa but also, ei2πa = (ei2π)a = 1a = 1 How to resolve the apparent contradiction?Homework Equations eab = (ea)b eix = cos x + i sin xThe Attempt at a Solution No clue... -

High School What is the name of this operation? (Inverse Exponent?)
So this puzzle has been wandering the internet. I find it unsolvable because there is no way to determine what operation is being performed to the double fries. Everyone assumes it is addition, but addition and multiplication are performed with signs elsewhere in the puzzle. If we assume that...- Algr
- Thread
- Exponent
- Replies: 11
- Forum: General Math
-

MHB Solving Complex Number With Negative Fractional Exponent: i^(-21/2)
Kindly help me with this. Solve i^(-21/2) Note: i means iota.- Asawira Emaan
- Thread
- Complex Complex number Exponent fractional Negative
- Replies: 6
- Forum: Topology and Analysis
-

MHB How do you solve a goofy exponent problem using logarithms?
$$3^x-14\cdot 3^{-x}=5$$ so expanded $$x\ln{3}-\ln 7-\ln 2 +x \ln 3=\ln 5$$ ok W|A says the answer is $$\frac{\ln\left({7}\right)}{\ln\left({3}\right)}$$ don't see the steps how?- karush
- Thread
- Exponent
- Replies: 9
- Forum: General Math
-

High School Triangle of Powers: Revolutionary Math Notation
Recently I saw this clip on YouTube which has a revolutionary idea of mathematical notations,What do you think about it?- YoungPhysicist
- Thread
- exponent log triangle
- Replies: 36
- Forum: General Math
-
R
MHB Finding Domain for Natural Log with Exponent f(x)=ln(x^2−5x)
I just asked a similar question, but I got help for that one, and now I am stumped again. I need to find the domain for $$f(x) = ln(x^2-5x)$$ What's confusing me is how to deal with the exponent. I can't think of a way to get around it.- RidiculousName
- Thread
- Domain Exponent Log Natural Natural log
- Replies: 6
- Forum: Calculus
-

High School Super basic polynomial and exponent definition help
Please bare with me. Most of you know I actually don't have a great math background. In any case I'm going way back and filling in some very basic math that I have long forgot. I have some questions about terms in a polynomial. Here is an example $$3x^5+7x^3-5$$ 1. From my book 3 and 7 are...- Greg Bernhardt
- Thread
- Definition Exponent Polynomial
- Replies: 15
- Forum: General Math
-
S
Undergrad Consequences on a system of ODEs after performing operations
Hi, I have derived a matrix from a system of ODE, and the matrix looked pretty bad at first. Then recently, I tried the Gauss elimination, followed by the exponential application on the matrix (e^[A]) and after another Gauss elimination, it turned "down" to the Identity matrix. This is awfully...- SeM
- Thread
- Elimination Exponent Matrix Ode Odes Operations System
- Replies: 4
- Forum: Linear and Abstract Algebra
-
R
Coupled differential equations using matrix exponent
Homework Statement Solve the following coupled differential equations by finding the eigenvectors and eigenvalues of the matrix and using it to calculate the matrix exponent: $$\frac{df}{dz}=i\delta f(z)+i\kappa b(z)$$ $$\frac{db}{dz}=-i\delta b(z)-i\kappa f(z)$$ In matrix form...- roam
- Thread
- Coupled Differential Differential equations Exponent Matrix
- Replies: 11
- Forum: Calculus and Beyond Homework Help
-
A
How do you compute an exponent with irrational values?
Homework Statement Let's say I want to compute ##2^{2.4134}##. We know that the base is a rational number and the power is an irrational number. Please keep in mind that I have not taken too many math classes yet and I am self-studying right now by making a calculator and respective algorithms...- Arnoldjavs3
- Thread
- Exponent Irrational
- Replies: 14
- Forum: Calculus and Beyond Homework Help
-
H
How to find a constant in this quadratic equation?
Homework Statement Homework Equations for equation which has 2 different solutions, D >0 The Attempt at a Solution (1)[/B] D > 0 b^2 - 4ac > 0 3 - 4root2.k > 0 k < 3 / ( 4root 2 ) k < ( 3 root 2 ) /8 has solution of sin tetha and cos tetha sin 0 = 0, cos 0 = 1. when x = 0, and x = 1 -->...- Helly123
- Thread
- Constant Exponent Quadratic Quadratic equation Quadratic equations
- Replies: 10
- Forum: Precalculus Mathematics Homework Help
-
Exponential and logarithmic Equation Problems
Homework Statement Evaluate each of the following expressions without using a calculator. 1) log216√8Solve for the unknown value in each of the following equations without using a calculator. 2) 3(x+4)−5(3x)=684 3) 7(42x)=28(4x) Homework Equations Exponent law for multiplication The...- onemic
- Thread
- Exponent Exponential Logarithmic Logarithms
- Replies: 12
- Forum: Precalculus Mathematics Homework Help
-

Graduate Estimation of Hurst Exponent Using Rescaled Range
Hey folks, long time no see! :woot: I am trying to estimate the Hurst Exponent for financial data using the R/σ (Rescaled Range) method. I have no authoritative source for this method. All I have are web pages (and we know how accurate those are). Specifically, I've been using the following...- quantumdude
- Thread
- Estimation Exponent Range
- Replies: 5
- Forum: Set Theory, Logic, Probability, Statistics
-

Undergrad Proving an exponent law in group theory
The textbook proves that ##x^a x^b = x^{a+b}## by an induction argument on b. However, is an induction argument really necessary here? Can't we just look at the LHS and note that there are a ##a## x's multiplied by ##b## x's, so there must be ##a+b## x's?- Mr Davis 97
- Thread
- Exponent Group Group theory Law Theory
- Replies: 5
- Forum: Linear and Abstract Algebra
-
Z
MHB Logarithm and Exponent Question
I'm confused on this question. The equation m log p (n) = q can be written in exponential form as.. The answer on the work sheet is p^(q/m)=n but shouldn't it be P^(qm) = n ? According to the power rule? My teacher explained this by writing down for me log p (n) = q / m but I'm confused here- zekea
- Thread
- Exponent Logarithm
- Replies: 4
- Forum: General Math
-
M
MHB Exponent of Group Hey! :o - Answers to Questions
Hey! :o For each group $G$, $\text{exp}(G)$ is the exponent of the group $G$, i.e., the smallest positive integer $k$, such that $g^k=e$ for each $g\in G$. Let $G$ be a finite group. I have shown that $\text{exp}(G)$ divides $|G|$, and if $G$ is cyclic, then $\text{exp}(G)=|G|$, as follows...- mathmari
- Thread
- Exponent Group
- Replies: 16
- Forum: Linear and Abstract Algebra
-

Calculating the definite integral using FTC pt 2
Homework Statement Sorry that I am not up on latex yet, but will describe the problem the best I can. On the interval of a=1 to b= 4 for X. ∫√5/√x. Homework EquationsThe Attempt at a Solution My text indicates the answer is 2√5. I have taken my anti derivative and plugged in b and subtracted...- Cjosh
- Thread
- Calculus Definite integral Definite integrals Exponent Fundamental theorem Integral
- Replies: 9
- Forum: Calculus and Beyond Homework Help
-

Pulling fractional exponents out of an expression
Homework Statement Find critical numbers of the function: F(x)=t^3/4 - 2t^1/4 Derivative I got: F'(x)=3/4 t^-1/4 - 1/2 t^-3/4 Homework EquationsThe Attempt at a Solution I have found the derivative and I understand I must pull out a t in order to find critical numbers, and run across this...- Cjosh
- Thread
- Algebra Calc 1 Critical points Exponent Exponents Expression fractional Fractional exponents
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-

Undergrad Understanding Lyapunov Exponent: Why Do We Use an Exponential Function?
Hey guys, I need your help. I am not sure if this is the right part of the forum to ask this question. So I started reading papers about the Lyapunov Exponent, but there is something I do not understand in the formula. Why ? It seems logical that we want because we want to get the Exponent...- ATY
- Thread
- Exponent Exponential function Lyapunov Ocean
- Replies: 1
- Forum: Other Physics Topics
-
E
Undergrad Why time in formula accelarion has exponent two
hello folks, I am learning about how create a equation dimensional to formula Force (m*a). I know this formula written this way: [F]=[ma] where: m=mass a=acceleration -> L/T² The result is [F] = M * (L/T²) * L⁰ My result it's right? Why T, relative time, has exponent two in formula... -
K
Relative uncertainty (negative exponent)
Homework Statement A distance R is measured to be 3.400±0.003m. What is the relative uncertainty in R? 9×10-4 What is the relative uncertainty in R^-2? Homework EquationsThe Attempt at a Solution Relative uncertainty of R is 0.003/3.4=8.8e-4 Relative uncertainty of R^-2= -2(8.8e-4)=-1.76e-3...- KevinFan
- Thread
- Exponent Relative Uncertainty
- Replies: 2
- Forum: Introductory Physics Homework Help
-
T
MHB Derivative of function with a natural log in the exponent
Supposing we have $f(x) = {2}^{lnx}$, how would we find $f'(x)$? -
B
MHB Solve Exponent Problem: 3^x=4^y=12^z
Given 3^x=4^y =12^z show that $$z=\frac{xy}{x+y}$$ I've take logs on both sides and find myself going in circles, any hints?- Bushy
- Thread
- Exponent
- Replies: 1
- Forum: General Math
-

Exponential having ln exponent
Homework Statement How is ## e^log√(1-x^2)## equal to ##√(1-x^2)?##Homework EquationsThe Attempt at a Solution taking ln on the function, ln√(1-x^2). lne⇒ ln√(1-x^2) ....- chwala
- Thread
- Exponent Exponential Ln
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-

Undergrad Standard notation needed for binary numbers as exponents
I work a lot in binary. I am organizing some of my work and need a way to write expressions. I can always create my own notation, but i would rather not invent something that already exists. 1011 is binary for 11 base 10. I use this {3,1,0} to represent the binary with just exponents. When I...- coolul007
- Thread
- Binary Exponent Exponents Notation Numbers Standard
- Replies: 9
- Forum: Set Theory, Logic, Probability, Statistics
-
S
Help to understand polytropic exponent and efficiency
Hello all, I am new to thermodynamics applied to turbines and compressors and I am trying to get my head around what is represented when calculating the work of a compression/expansion process using the polytropic exponent as oppose to the specific heat ratio of 1.4 (I'm working with air). The...- Sorade
- Thread
- Compressor Efficiency Exponent Polytropic Turbine
- Replies: 3
- Forum: Mechanical Engineering
-
B
Proving the Exponent Laws in Group Theory
Homework Statement Let ##x \in G## and ##a,b \in \mathbb{Z}^+## Prove that ##x^{a+b} = x^a x^b##. Homework EquationsThe Attempt at a Solution If I am not mistaken, we would have to do multiple induction on ##a## and ##b## for the statement/proposition ##P(a,b) : x^{a+b} = x^a x^b##. First we...- Bashyboy
- Thread
- Exponent Group Group theory Laws Theory
- Replies: 14
- Forum: Calculus and Beyond Homework Help
-
Z
Undergrad Differentiating an exponential with a complex exponent
Hello, folks. I'm trying to figure out how to take the partial derivative of something with a complex exponential, like \frac{\partial}{\partial x} e^{i(\alpha x + \beta t)} But I'm not really sure how to do so. I get that since I'm taking the partial w.r.t. x, I can treat t as a constant term...- Zacarias Nason
- Thread
- Complex Differentiating Exponent Exponential
- Replies: 7
- Forum: Differential Equations
-

Understanding Exponent Multiplication: cnxn-1
Homework Statement x(cnxn-1) 3. The Attempt at a Solution I know that the answer is cnxn I'm not sure why though. My thinking is that we have cnxn-1 and we multiply that by x. x times x is x2 so I'm expecting a 2 to interact with the n-1 in the exponents. I'm just not sure how n-1 interacts...- PhysicsBoyMan
- Thread
- Exponent Exponents Multiplication
- Replies: 5
- Forum: Precalculus Mathematics Homework Help
-
D
Undergrad Greatest common factor with exponents of first input
ok so is there a function that exists (for all intents and purposes let's call it G(x,y) )where x= a^2*b^4*c y=a^4*b^2*d G(x,y) = a^2*b^4 basically gcd, but the exponents match those of the common prime factors of the first input (x) ******** equally useful would be a function where the...- DirichletHole
- Thread
- Exponent Exponents Factorization Greatest common divisor Input
- Replies: 4
- Forum: General Math
-
M
Laws of Exponents: Solve Math Homework Questions
Hello, this isn't really a physics question but I'm getting pretty desperate and you guys have always been able to help me out before :) 1. Homework Statement http://imgur.com/mYtJDLI Homework Equations I believe I'm suppose to use the Laws of Exponents. For the first set possibly but not...- Meezus
- Thread
- Exponent Exponents Laws Power
- Replies: 22
- Forum: Precalculus Mathematics Homework Help
-
C
How Do You Solve the Equation 4^(x-1) = 2^x + 8?
Homework Statement Solve the equation 4^{x-1} = 2^x + 8. Homework Equations Just algebra The Attempt at a Solution 4^{x-1} = 2^x + 8 2^{2(x-1)} = 2^x + 2^3 2^{2x}2^{-2} = 2^x + 2^3 \frac{2^{2x}}{2^2} = 2^x + 2^3 2^{2x} = 2^22^x + 2^5 2^x2^x - 2^22^x = 2^5 2^x(2^x - 2^2) = 2^5 I...- cmkluza
- Thread
- Exponent
- Replies: 4
- Forum: Precalculus Mathematics Homework Help
-
G
Rational exponents (was: Math Discussion)
Homework Statement (-64)^(3/2) Homework Equations None. The Attempt at a Solution There is no answer that can be reached and it is supposed not be a real number. I was wondering why that is. How is it that there is no "real" answer to this problem?- goolalklk
- Thread
- Discussion Exponent Exponents Rational
- Replies: 5
- Forum: Precalculus Mathematics Homework Help