What is Inequality: Definition and 1000 Discussions

In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side. This statement permits the inclusion of degenerate triangles, but some authors, especially those writing about elementary geometry, will exclude this possibility, thus leaving out the possibility of equality. If x, y, and z are the lengths of the sides of the triangle, with no side being greater than z, then the triangle inequality states that




z
≤
x
+
y
,


{\displaystyle z\leq x+y,}
with equality only in the degenerate case of a triangle with zero area.
In Euclidean geometry and some other geometries, the triangle inequality is a theorem about distances, and it is written using vectors and vector lengths (norms):




‖

x

+

y

‖
≤
‖

x

‖
+
‖

y

‖
,


{\displaystyle \|\mathbf {x} +\mathbf {y} \|\leq \|\mathbf {x} \|+\|\mathbf {y} \|,}
where the length z of the third side has been replaced by the vector sum x + y. When x and y are real numbers, they can be viewed as vectors in R1, and the triangle inequality expresses a relationship between absolute values.
In Euclidean geometry, for right triangles the triangle inequality is a consequence of the Pythagorean theorem, and for general triangles, a consequence of the law of cosines, although it may be proven without these theorems. The inequality can be viewed intuitively in either R2 or R3. The figure at the right shows three examples beginning with clear inequality (top) and approaching equality (bottom). In the Euclidean case, equality occurs only if the triangle has a 180° angle and two 0° angles, making the three vertices collinear, as shown in the bottom example. Thus, in Euclidean geometry, the shortest distance between two points is a straight line.
In spherical geometry, the shortest distance between two points is an arc of a great circle, but the triangle inequality holds provided the restriction is made that the distance between two points on a sphere is the length of a minor spherical line segment (that is, one with central angle in [0, π]) with those endpoints.The triangle inequality is a defining property of norms and measures of distance. This property must be established as a theorem for any function proposed for such purposes for each particular space: for example, spaces such as the real numbers, Euclidean spaces, the Lp spaces (p ≥ 1), and inner product spaces.

View More On Wikipedia.org
Recent contents Top users
  1. anemone

    MHB Inequality of logarithm function

    Prove that, for all real $a,\,b,\,c$ such that $a+b+c=3$, the following inequality holds: $\log_3(1+a+b)\log_3(1+b+c)\log_3(1+c+a)\le 1$
  2. anemone

    MHB Inequality Challenge: Prove $\ge 0$ for All $a,b,c$

    Prove \frac{a-\sqrt{bc}}{a+2b+2c}+\frac{b-\sqrt{ca}}{b+2c+2a}+\frac{c-\sqrt{ab}}{c+2a+2b}\ge 0 holds for all positive real $a,\,b$ and $c$.
  3. M

    MHB Inequality related to number of p-Sylow subgroups

    Hey! :o I want to show that if $G$ is finite and $f:G\rightarrow H$ is a group epimorphism then $|\text{Syl}_p(G)|\geq |\text{Syl}_p(H)|$. I have done the following: Since $f:G\rightarrow H$ is a group epimorphism, from the first isomorphism theorem we have that $H$ is isomorphism to $G/\ker...
  4. Albert1

    MHB Inequality Challenge: Prove $\sum_{1}^{n}$

    $n\in N,n\geq 2$ prove: $ \sum_{1}^{n}(\dfrac{1}{2n-1}-\dfrac{1}{2n})>\dfrac {2n}{3n+1}$
  5. anemone

    MHB Prove Inequality of $x$ and $y$ with $x^3-y^3=2$ and $x^5-y^5\ge 4$

    $x$ and $y$ are two real numbers such that $x^3-y^3=2$ and $x^5-y^5\ge 4$. Prove that $x^2+y^2\gt 2$.
  6. dbertels

    B Bell's Inequality && polarisation for the layman

    My previous thread on this topic got a bit messy as the gist of the argument was in the middle of the thread and turned out wrong. Hence this new updated version. One of my favourite articles on Bell's Theorem can be found at...
  7. anemone

    MHB Inequality challenge for all positive (but not zero) real a, b and c

    Prove \frac{ab}{a+b+ab}+\frac{bc}{b+c+bc}+\frac{ca}{c+a+ca}\le \frac{a^2+b^2+c^2+6}{9} for all positive real $a,\,b$ and $c$ and $a,\,b,\,c\ne 0$.
  8. dbertels

    B Proving entanglement using polarisation & Bell's Inequality

    I've seen some articles using particle spin experiments to 'prove' that the results violate Bell's inequality and consequently local reality. I've also seen stated that the same experiments can be done using other particle attributes such as polarisation. I can see how with polarisation, you...
  9. D

    Discover the form of real solution set

    Homework Statement ##|4^{3x}-2^{4x+2}*3^{x+1}+20*12^x*3^x| > 8*6^x(8^{x-1}+6^x)## For some numbers ##a, b, c, d## such that ##-\infty < a <b < c <d < +\infty ## the real solution set to the given inequality is of the form ##(-\infty, a] \cup [b, c] \cup [d, +\infty)## Prove it by arriving at...
  10. anemone

    MHB Can Inequality be Proven for Positive Reals a and b?

    Prove that \frac{\sqrt{a^2+b^2}}{a+b}+\sqrt{\frac{ab}{a^2+b^2}}\le \sqrt{2} for all positive reals $a$ and $b$.
  11. P

    Proving Inequality: Can Partial Derivatives Help?

    Hello! Say we have an inequality that says that ##f(x, y)>c## where ##f(x, y)## is a function of two variables and ##c## is a constant. Assume that we know this inequality to be true when ##x=a## and ##y=b##. If you show that the partial derivatives of ##f(x, y)## with respect to ##x## and ##y##...
  12. C

    MHB Proving an absolute value inequality

    If $\left| a \right| \le b$, then $-b\le a\le b$. Let $a,b \in\Bbb{R}$ The definition of the absolute value is $ \left| x \right|= x, x\ge 0$ and $\left| x \right|=-x, x< 0$, where x is some real number. Case I:$a\ge 0$, $\left| a \right|=a>b$ Case II: a<0, $\left| a \right|=-a<b$the solution...
  13. entropy1

    Understanding Bell's inequality

    I am not sure if I am allowed to ask this, but here's my shot: I find all the explanations of Bell's theorem summed up here, very different in interpretation and also (for me) incomprehensible. I have these simple questions: How does the Bell inequality, stated as N(A, not B) + N(B, not C) ≥...
  14. J

    MHB Proving inequality: Can we show n^n * (n+1)/2)^2n ≥ (n+1)/2)^3?

    How can we prove $$n^n\cdot \left(\frac{n+1}{2}\right)^{2n}\geq \left(\frac{n+1}{2}\right)^3$$ I did not understand from where i have start.
  15. P

    Regarding Schwartz inequality and integration bounds

    Based on Schwartz inequality, I am trying to figure out why there should/can be the "s" variable which is the lower bound of the integration in the RHS of the following inequality: ## \left \|\int_{-s}^{0} A(t+r)Z(t+r) dr \right \|^{2} \leq s\int_{-s}^{0}\left \| A(t+r)Z(t+r) \right \|^{2} dr...
  16. anemone

    MHB Proving Inequality Challenge: $a,\,b,\,c$ | Real Numbers

    Let $a,\,b,\,c$ be real numbers such that $a\ge b\ge c>0$. Prove that \frac{a^2-b^2}{c}+\frac{c^2-b^2}{a}+\frac{a^2-c^2}{b}\ge 3a-4b+c.
  17. anemone

    MHB Proving Inequality for Positive Real Numbers

    For positive real numbers $a,\,b,\,c$, prove the inequality: a + b + c ≥ \frac{a(b + 1)}{a + 1} + \frac{b(c + 1)}{b + 1}+ \frac{c(a + 1)}{c + 1}
  18. anemone

    MHB Inequality challenge for positive real numbers

    If $a$ and $b$ are two positive real, and that $a^3+b^3=a-b$, prove that $2\left(\sqrt{2}-1\right)a^2-b^2\lt 1$.
  19. D

    Find the sets of real solutions

    [b[1. Homework Statement [/b] ##|4^{3x}-2^{4x+2}*3^{x+1}+20*12^x*3^x| \ge 8*6^x(8^{x-1}+6^x)## The sets containing the real solutions for some numbers ##a, b, c, d,## such that ##-\infty < a < b < c < d < +\infty## is of the form ##(-\infty, a] \cup [b, c] \cup [d, +\infty)##. Prove it by...
  20. Alpharup

    Can b always be greater than 0?

    Let a>0. It is also true that a+b>0. Can we prove that b>0 always? My attempt b>-a... but 0>-a. therefore min (b,0)>-a case 1: b <0. If, b <-a, then a <-b so a+b <b-b so, a+b <0. Contradiction Hence b>0. Is my proof right?
  21. N

    The how to represent an inequality in a graph question

    if x+y ≥ 2 it contains all the point in the line x+y =2 and the half plane above it. but ,graph if x-y ≥ 2 then if consider a line x-y= 2 the inequality represents the line and the half plane below it . i don't understand why it represents the half line below it why not above ?
  22. J

    Inequality involving probability of stationary zero-mean Gaussian

    Homework Statement Let $$(X(n), n ∈ [1, 2])$$ be a stationary zero-mean Gaussian process with autocorrelation function $$R_X(0) = 1; R_X(+-1) = \rho$$ for a constant ρ ∈ [−1, 1]. Show that for each x ∈ R it holds that $$max_{n∈[1,2]} P(X(n) > x) ≤ P (max_{n∈[1,2]} X(n) > x)$$ Are there any...
  23. anemone

    MHB Can $\sqrt{8}^{\sqrt{7}}$ Ever Be Greater Than $\sqrt{7}^{\sqrt{8}}$?

    Prove that $\sqrt{8}^{\sqrt{7}}<\sqrt{7}^{\sqrt{8}}$.
  24. samalkhaiat

    Schwarz Inequality is your friend

    I would like to show you how to use Schwarz inequality to prove some important general theorems and solve problems about vectors in Minkowski spacetime. Okay, Schwarz inequality states that \left| U^{k}V^{k}\right| \leq \sqrt{(U^{i})^{2}(V^{j})^{2}}. \ \ i,j,k =1,2,3 \ \ \ (1) And, the...
  25. S

    Riemannian Penrose Inequality: Proof Restriction to n=3?

    I am reading the proof of the Riemannian Penrose Inequality (http://en.wikipedia.org/wiki/Riemannian_Penrose_inequality) by Huisken and Ilmamen in "The Inverse Mean Curvature Flow and the Riemannian Penrose Inequality" and I was wondering why they restrict their proof to the dimension ##n=3##...
  26. E

    MHB Why Does an Inequality Sign Flip?

    Why would an inequality sign flip in an answer. For example: 16 < -s -6 The answer is given s < -22 I had -s > 22 I am thinking it is because when you x by -1 to keep from having a negative variable the inequality sign flips...is this why?
  27. Albert1

    MHB Prove Inequality: $m,n,k\in N$, $m>1,n>1$

    $m,n,k\in N$, and $m>1,n>1$ prove : $(3^{m+1}-1)\times (5^{n+1}-1)\times(7^{k+1}-1)>98\times 3^m\times 5^n\times7^k$
  28. T

    Explaining John Bell & Anton Zeilinger's Attempt to Prove No Definite Reality

    I was wondering if someone could explain to me how John Bell and Anton Zeilinger have attempted to prove there is no definite reality in the sub-atomic world. How could it ever be proven there are no hidden variables that humans just don't or can't know about? If I am not mistaken, Einstein for...
  29. Zafa Pi

    Is there a Bell type inequality involving only three values?

    There are several Bell inequalities involving 4 values (e.g. CHSH where they are sometimes denoted by Q, R, S, T). The original Bell inequality involved 6. All being refuted by QM. Is it known whether there is one with only 3 values? I can prove there isn't one with 2 values.
  30. anemone

    MHB Inequality Challenge: Prove Real $a,b,c,x,y,z$

    Prove for all positive real $a,\,b,\,c,\,x,\,y,\,z$ that $\dfrac{a^3}{x}+\dfrac{b^3}{y}+\dfrac{c^3}{z}\ge \dfrac{(a+b+c)^3}{3(x+y+z)}$.
  31. T

    MHB Beginner Exercises on Prime numbers and Equality / Inequality proofs

    Does anyone know a good resource for exercises on these topics?
  32. MarkFL

    MHB Prove Summation Inequality: $\frac{1}{2n-1} > \sum_{k=n}^{2n-2}\frac{1}{k^2}$

    Prove the following: \sum_{k=n}^{2n-2}\frac{1}{k^2}<\frac{1}{2n-1} where 2\le n
  33. anemone

    MHB Prove Inequality for $a,\,b,\,c$: $9abc\ge7(ab+bc+ca)-2$

    Let $a,\,b$ and $c$ be positive real numbers satisfying $a+b+c=1$. Prove that $9abc\ge7(ab+bc+ca)-2$.
  34. W

    Number of non negative integer solutions to this inequality

    Homework Statement How many non-negative integer solutions are there to the equation x1 + x2 + x3 + x4 + x5 < 11, (i)if there are no restrictions? (ii)How many solutions are there if x1 > 3? (iii)How many solutions are there if each xi < 3? Homework Equations N/A The Attempt at a Solution...
  35. AlexOliya

    Proving an Inequality: A Scientific Approach

    Homework Statement Homework Equations With the regards to posting such a incomplete equation, I will soon put in the updated one Thank you The Attempt at a Solution visual graph... didn't help
  36. anemone

    MHB Can inequality be proven with positive real numbers and fractions?

    For the positive real numbers $x,\,y$ and $z$ that satisfy $\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=3$, prove that $\dfrac{1}{\sqrt{x^3+1}}+\dfrac{1}{\sqrt{y^3+1}}+\dfrac{1}{\sqrt{z^3+1}}\le \dfrac{3}{\sqrt{2}}$.
  37. S

    MHB Parametric Inequality: Find b to Solve x^4-2x^2<a^2-1

    yesterday i come across the following inequality; Given a>0 find a b>o such that ; If 2-b<x<\frac{1}{4}+b,then x^4-2x^2<a^2-1 Can anybody help where to start from??
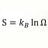
  38. morrobay

    Hidden variables and Bell's inequality

    [Mentor's note: Moved from a thread about field theories as this is just about the basic meaning of the theorem for ordinary entangled particles]] Suppose that there are photon spin outcomes that are pre existing from entanglement or from local hidden variables. For every detector angle...
  39. W

    Cantelli's Inequality and Chebyshev's Inequality

    Homework Statement The number of customers visiting a store during a day is a random variable with mean EX=100and variance Var(X)=225. Using Chebyshev's inequality, find an upper bound for having more than 120 or less than 80customers in a day. That is, find an upper bound on P(X≤80 or X≥120)...
  40. W

    Markov's Inequality for Geometric Distribution.

    Homework Statement Let X∼Geometric(p). Using Markov's inequality find an upper bound for P(X≥a), for a positive integer a. Compare the upper bound with the real value of P(X≥a). Then, using Chebyshev's inequality, find an upper bound for P(|X - EX| ≥ b). Homework Equations P(X≥a) ≤ Ex / a...
  41. anemone

    MHB Prove Inequality Challenge for $a\in \Bbb{Z^+}$

    Let $a\in \Bbb{Z^+}$, prove that $\dfrac{2}{2-\sqrt{2}}>\dfrac{1}{1\sqrt{1}}+\dfrac{1}{2\sqrt{2}}+\dfrac{1}{3\sqrt{3}}+\cdots+\dfrac{1}{a\sqrt{a}}$.
  42. A

    Is (∞ - 1) < ∞ True for Inequalities with Infinity?

    Is this true? (∞ - 1) < ∞
  43. B

    Triangle inequality implies nonnegative scalar multiple

    I'm not really sure if this is true, which is why I want your opinion. I have been trying to prove it, but it will help me a lot if someone can confirm this. Let ## v_{1}, v_{2} ... v_{n} ## be vectors in a complex inner product space ##V##. Suppose that ## | v_{1} + v_{2} +...+ v_{n}| =...
  44. Steve Turchin

    Spivak's Calculus (4th ed): Chapter 1 Problem *21 Inequality

    Homework Statement Prove that if ## |x-x_0|<\min (\frac {\epsilon}{2(|y_0|+1)},1)## and ##|y-y_0|<\frac{\epsilon}{2(|x_0|+1)} ## then ## |xy-x_0y_0|<\epsilon ## Homework Equations N/A The Attempt at a Solution From the first inequality I can see that: ## |x-x_0|<\frac...
  45. M

    MHB How to prove an inequality with a direct proof?

    Hello, I'm having trouble with an assigned problem, not really sure where to begin with it: Prove that if a \in R and b \in R such that 0 < b < a, then {a}^{n} - {b}^{n} \le {na}^{n-1}(a-b), where n is a positive integer, using a direct proof. Pointers or the whole proof would be appreciated...
  46. A

    Stuck on Proof by induction of 2^n>n^3 for all n>=10

    Homework Statement Using the principle of mathematical induction, prove that for all n>=10, 2^n>n^3 Homework Equations 2^(n+1) = 2(2^n) (n+1)^3 = n^3 + 3n^2 + 3n +1 The Attempt at a Solution i) (Base case) Statement is true for n=10 ii)(inductive step) Suppose 2^n > n^3 for some integer >=...
  47. P

    When is the Cauchy-Schwartz inequality as large as possible?

    The Cauchy-Schwartz inequality (\sum_{i=1}^n x_i^2)(\sum_{i=1}^n y_i^2) - (\sum_{i=1}^n x_iy_i)^2 \geq 0 holds with equality (or is as "small" as possible) if there exists an a \gt 0 such that x_i=ay_i for all i=1,...,n . But when is the inequality as "large" as possible? That is, can we...
  48. C

    MHB Interval Notation of Inequality: -9<1/x<=1

    I need help determining the interval notation of the inequality below: -9<1/x<=1
  49. Steve Turchin

    Complex absolute value inequality

    Solve the following inequality. Represent your answer graphically: ## |z-1| + |z-5| < 4 ## Homework Equations ## z = a + bi \\ |x+y| \leq |x| + |y| ## Triangle inequality The Attempt at a Solution ## |z-1| + |z-5| < 4 \\ \\ x = z-1 \ \ , \ \ y = z-5 \\ \\ |z-1+z-5| \leq |z-1| + |z-5| \\...
  50. O

    MHB Triangle Inequality and Convergence of ${y}_{n}$

    Let ${y}_{n}$ be a arbitrary sequence in X metric space and ${y}_{m+1}$ convergent to ${x}^{*}$ in X...İn this case by using triangle inequality can we say that ${y}_{n}\to {x}^{*}$
Back
Top