Metalsonic75
- 28
- 0
33.6 There is a ccw-induced current in the conducting loop shown in the figure. Is the magnetic field inside the loop increasing in strength, decreasing in strength, or steady?
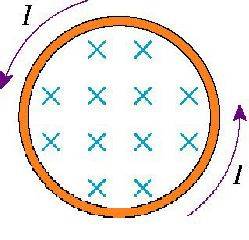
I don’t understand if the problem is referring to the induced magnetic field or the pre-existing magnetic field. I know that the induced field will increase, but I’m pretty sure the original electric field remains steady. Which one is the problem asking for?
I appreciate your help.
I don’t understand if the problem is referring to the induced magnetic field or the pre-existing magnetic field. I know that the induced field will increase, but I’m pretty sure the original electric field remains steady. Which one is the problem asking for?
I appreciate your help.