Dafe
- 144
- 0
1. The problem statement and attempt at solution
Given the matrix S_ij and a_i evaluate a),b),c),d) and e)
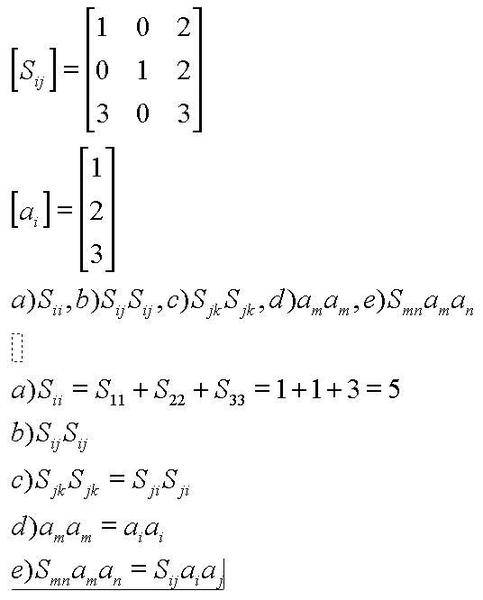
For a) I think i use Einsteins convention.
b) I just first sum on i, and then on j giving me 9 terms. The answer I get is 24.
d) can i change m with i since they are both dummy indexes?
e) the same problem as d I guess, is this allowed?
I'm trying to learn continuum mechanics by my self, and this is the first step.
Thank you.
Given the matrix S_ij and a_i evaluate a),b),c),d) and e)
For a) I think i use Einsteins convention.
b) I just first sum on i, and then on j giving me 9 terms. The answer I get is 24.
d) can i change m with i since they are both dummy indexes?
e) the same problem as d I guess, is this allowed?
I'm trying to learn continuum mechanics by my self, and this is the first step.
Thank you.