chavic
- 9
- 0
On this assignment I could do most of the work easily, I just have some questions on three problems
3. Homework Statement
A playground merry-go-round of radius R = 2.00 m has a moment of inertia I = 270 kg·m2 and is rotating at 9.0 rev/min about a frictionless vertical axle. Facing the axle, a 26.0 kg child hops onto the merry-go-round and manages to sit down on its edge. What is the new angular speed of the merry-go-round?3. Relevant equations
L=rmvsin[\theta]
I=.5MR^{2}
\omega= v/r
I attempted to use conservation of momentum.
I=.5MR^{2}
Solve for M (mass of merry-go-round)
I/.5R^{2}=M
M=135 kg
Angular velocity
Circumference of merry-go-round=12.5664 m
12.5664 * 9
Initial velocity=113.0976
Initial Momentum
L=rmv
=2(135)(133.09760)
Li=30536.352
So final momentum should be the same
L=rmv
v=L/rm
30536.352/ 2(162)=94.248
This is wrong
A wooden block of mass M resting on a frictionless, horizontal surface is attached to a rigid rod of length and of negligible mass. The rod is pivoted at the other end. A bullet of mass m traveling parallel to the horizontal surface and perpendicular to the rod with speed v hits the block and becomes embedded in it.
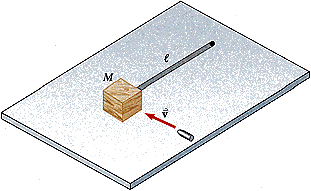 (a) What is the angular momentum of the bullet- block system? (For the following answers, use M for the mass M, m for the mass m, and L for the length .)
(a) What is the angular momentum of the bullet- block system? (For the following answers, use M for the mass M, m for the mass m, and L for the length .)
(b) What fraction of the original kinetic energy is converted into internal energy in the collision?
4. Relevant equations
? If someone could just point me in the right direction4. The attempt at a solution
Two astronauts, each having a mass of 70.0 kg, are connected by a 9.5 m rope of negligible mass. They are isolated in space, orbiting their center of mass at speeds of 5.50 m/s.
 (a) Treating the astronauts as particles, calculate the magnitude of the angular momentum.
(a) Treating the astronauts as particles, calculate the magnitude of the angular momentum.
(b) Calculate the rotational energy of the system.
(c) By pulling on the rope, one of the astronauts shortens the distance between them to 5.00 m. What is the new angular momentum of the system?
(d) What are the astronauts' new speeds?
(e) What is the new rotational energy of the system?
(f) How much work does the astronaut do in shortening the rope?
5. Relevant equations
L=mrvsin[\theta]
KE=.5I\omega^{2}
Work=\DeltaKE
I=MR^{2}
\omega= v/r5. The attempt at a solution
I have the answers for a-e, but I'm having a hard time with f
A=3657.5 kg·m^{2}/s
B=2117.5193 J
C=3657.5 kg·m^{2}/s
D=10.5 m/s
E=7717.5 J
*fixed momentums
So F should be
Work=\DeltaKE
or 7717.5-2117.5193=5599.9807
But this is the wrong answer
*I figured it out, its supposed to be in Kj
3. Homework Statement
A playground merry-go-round of radius R = 2.00 m has a moment of inertia I = 270 kg·m2 and is rotating at 9.0 rev/min about a frictionless vertical axle. Facing the axle, a 26.0 kg child hops onto the merry-go-round and manages to sit down on its edge. What is the new angular speed of the merry-go-round?3. Relevant equations
L=rmvsin[\theta]
I=.5MR^{2}
\omega= v/r
The Attempt at a Solution
I attempted to use conservation of momentum.
I=.5MR^{2}
Solve for M (mass of merry-go-round)
I/.5R^{2}=M
M=135 kg
Angular velocity
Circumference of merry-go-round=12.5664 m
12.5664 * 9
Initial velocity=113.0976
Initial Momentum
L=rmv
=2(135)(133.09760)
Li=30536.352
So final momentum should be the same
L=rmv
v=L/rm
30536.352/ 2(162)=94.248
This is wrong
--------------------------------------------------------------------
4. Homework Statement A wooden block of mass M resting on a frictionless, horizontal surface is attached to a rigid rod of length and of negligible mass. The rod is pivoted at the other end. A bullet of mass m traveling parallel to the horizontal surface and perpendicular to the rod with speed v hits the block and becomes embedded in it.
(b) What fraction of the original kinetic energy is converted into internal energy in the collision?
4. Relevant equations
? If someone could just point me in the right direction4. The attempt at a solution
--------------------------------------------------------------------
5. Homework Statement Two astronauts, each having a mass of 70.0 kg, are connected by a 9.5 m rope of negligible mass. They are isolated in space, orbiting their center of mass at speeds of 5.50 m/s.
(b) Calculate the rotational energy of the system.
(c) By pulling on the rope, one of the astronauts shortens the distance between them to 5.00 m. What is the new angular momentum of the system?
(d) What are the astronauts' new speeds?
(e) What is the new rotational energy of the system?
(f) How much work does the astronaut do in shortening the rope?
5. Relevant equations
L=mrvsin[\theta]
KE=.5I\omega^{2}
Work=\DeltaKE
I=MR^{2}
\omega= v/r5. The attempt at a solution
I have the answers for a-e, but I'm having a hard time with f
A=3657.5 kg·m^{2}/s
B=2117.5193 J
C=3657.5 kg·m^{2}/s
D=10.5 m/s
E=7717.5 J
*fixed momentums
So F should be
Work=\DeltaKE
or 7717.5-2117.5193=5599.9807
But this is the wrong answer
*I figured it out, its supposed to be in Kj
Last edited: