4 Variable K-Maps (reading and writing)

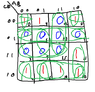
[dm41nes]

Homework Statement

We started K-Maps not too long ago, I have no idea how to read these or write these. I am only able to set them up, but as far as understanding prime implicants, max terms, min terms I feel I know nothing. Correct me if I am wrong, but 0's are max terms and 1's are min terms.

Homework Equations

This is not a Home work problem, I just put this together on paint.

The Attempt at a Solution

The farthest I get is grouping (horizontal, vertical). As for reading what I am doing, I am stumped.



Thank you in advance!

 

[berkeman]

You want to group the terms into the largest clumps that you can. What did you get for the simplest sum of minterms for that K-map?

 

[dm41nes]

You want to group the terms into the largest clumps that you can. What did you get for the simplest sum of minterms for that K-map?

Well my problem is I have no idea how to pull out the min or max terms or how to even read one for the matter. It doesn't really help that I do not own a book either.

Thank you for your prompt reply!

 

[berkeman]

Ah. This should help get you going:

http://en.wikipedia.org/wiki/Karnaugh_map

.

 

[jck_ccc]

Yes, minterms are 1 and maxterms are 0.

As far as I'm concerned, the K-map is mainly used to find the sum of minterms.

Just looking at the 1's in the chart, you can see that the original equation looked something like this:
f(x) = a'b'c'd' + a'bc'd' + ab'c'd' + ab'cd + abcd' + ab'cd' + a'bcd' + a'b'cd'

However, you can circle the ones to create a sum om minterms. Like berkeman said, you want to group the terms into the largest clumps you can. I've redrawn the K-map with colours for clarity:
-red: a'd'
-orange: b'd'
-blue: cd'
-green: ab'c
Inside each circled area, look for the values that do not change. For the red one, the circle covers 00 and 01 horizontally. The first digit represents the a, and because it is a 0 and not a 1, you get a'. Vertically, the red circle covers 00 and 10. The 2nd digit remains the same this time, and this one corresponds to d. As a result, you get d'. Finally, you put the a' and d' together to get a'd'.
Do that for the rest of the circled clumps and you should get the answers I listed above (unless I've made a mistake).

Your sum of minterms will be:
a'd' + b'd' + cd' + ab'c

Note the circles can only be of size 2^n (size 1, 2, 4, 8, 16).