Wow! Five equations for such an innocent looking circuit.
Thank you gneill for bringing some sanity to this topic!
Well, ILS has been guiding me through to get to these equations so I thought that makes sense and that he's probably making a point to me knowing him :)
It might of of interest to note that for a complete solution to a given circuit, it is sufficient to have a set of loops where each component of the circuit belongs to at least one loop.
That is indeed an interesting fact to note!
For this circuit, three loops (and thus three equations) suffice to completely solve the circuit for any given values of the its components. And in indeed, there are particular conditions imposed upon this example that allow you to eliminate one of the loops entirely, leaving just two loops and thus two equations and two unknowns to worry about. I refer, of course, to the fact that the problem specifies that the current in the ammeter loop is zero. It is also the case that the only voltage source in the circuit belongs to both remaining loops, the remainders of which consist of two resistors in series. So you end up with two equations that don't even need to be solved simultaneously!
Right! So if I solve the equation I made for the ammeter, it would naturally equal zero! I'd get zero = zero!
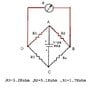
In the attached figure, note that the potential difference between the labeled points c and d is fixed by the battery. We are told that i3 is zero. This means that the currents i1 and i2 are entirely determined by the battery potential and the resistors of the given loop, and that these currents are entirely independent of each other -- the fixed battery voltage isolates one loop from the other, since no voltage variations can occur across an ideal voltage source.
We're dealing with basic electricity/circuits, I presume we're initially only dealing with ideal voltage sources?
Although, I have to say, I didn't know that it's because there is a fixed battery voltage that one loop can be isolated from the other.
So it remains to write the two equations for i1 and i2, and using i1 and i2, determine the potential at points a and b (with respect to d, say), and equate the potentials.
Wait a second! I agree with your i2 loop, but your i1 loop is opposite to what it should be, no? It goes from minus to plus!
One, you are always free to ground any point in the circuit
I'm not sure what you mean by "grounding any point in the circuit". Can you explain or provide me with at least a referrence link otherwise?
Two, there is no current through the ammeter which means don't worry about it.
If I had a system of garden hoses and I told you to find out how much gravel was in each garden hose (making a particular flow rate), and if one of these garden hose sections happened to have its pressure completely balanced so there was no flow, you'd leave it alone and just call it good (i.e. ignore the ammeter because it makes no sense to try to include it)
I had thought so initially! :) That's why in my initial suggestion where I started this topic I made 3 equations
without the ammeter.
*I'm not sure if I follow your garden hose analogy, but I'll think about it.
I'm kinda rushing this reply because I have to go and would probably only reply back tomorrow.
Thanks everyone! :)