Radius of Smallest Circle in 6 Circles Problem (10cm)

  • Thread starter Thread starter KKW
  • Start date Start date
  • Tags Tags
    Circles
AI Thread Summary
In the problem of inscribing four identical circles within a larger circle of radius 10 cm, the radius of the smaller central circle can be determined using geometric relationships. The radius of the four identical circles is calculated to be 10 cm divided by 3, resulting in approximately 3.33 cm. The smaller circle, which touches all four identical circles, has a radius that can be derived from the arrangement of these circles. The configuration allows for the determination of the radius of the smallest circle, which is approximately 1.11 cm. This geometric arrangement highlights the relationships between the radii of the circles involved.
KKW
Messages
3
Reaction score
0
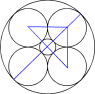
If you inscribe 4 circles inside a bigger circle and then add another smaller circle, touching the other 4 circles, what is the radius of the smallest circle (in the centre) if the radius of the biggest circle is 10cm?
 
Mathematics news on Phys.org
Is the radius of the four circles the same?
 
Assuming four circles are identical, that's everything you may need. Think how these are related to the radii of circles in question.
 

Attachments

  • 6_circles_question.png
    6_circles_question.png
    9.8 KB · Views: 495

Thread 'Trigonometry problem of interest'

Seemingly by some mathematical coincidence, a hexagon of sides 2,2,7,7, 11, and 11 can be inscribed in a circle of radius 7. The other day I saw a math problem on line, which they said came from a Polish Olympiad, where you compute the length x of the 3rd side which is the same as the radius, so that the sides of length 2,x, and 11 are inscribed on the arc of a semi-circle. The law of cosines applied twice gives the answer for x of exactly 7, but the arithmetic is so complex that the...
View full post »
Thread 'Unit Circle Double Angle Derivations'

Thread 'Unit Circle Double Angle Derivations'

Here I made a terrible mistake of assuming this to be an equilateral triangle and set 2sinx=1 => x=pi/6. Although this did derive the double angle formulas it also led into a terrible mess trying to find all the combinations of sides. I must have been tired and just assumed 6x=180 and 2sinx=1. By that time, I was so mindset that I nearly scolded a person for even saying 90-x. I wonder if this is a case of biased observation that seeks to dis credit me like Jesus of Nazareth since in reality...
View full post »
Thread 'Imaginary Pythagoras'

Thread 'Imaginary Pythagoras'

I posted this in the Lame Math thread, but it's got me thinking. Is there any validity to this? Or is it really just a mathematical trick? Naively, I see that i2 + plus 12 does equal zero2. But does this have a meaning? I know one can treat the imaginary number line as just another axis like the reals, but does that mean this does represent a triangle in the complex plane with a hypotenuse of length zero? Ibix offered a rendering of the diagram using what I assume is matrix* notation...
View full post »

Similar threads

I Geometry problem of interest with a 3-4-5 triangle
2
Replies
59
Views
2K
MHB Area of multiple circles inside a rectangle
Replies
3
Views
2K
B Inscribing a circle in an Oblique Square (Drafting)
Replies
9
Views
1K
I Equation for circle points in 3D
Replies
3
Views
3K
B The Pitcher's Mound
Replies
10
Views
2K
MHB AO+BO+CO≥6r where r is the radius of the inscribed circle
Replies
2
Views
1K
B Understanding why πr^2 works for different area calculations
Replies
7
Views
2K
MHB Calculating Geometric Probability on a Round Table
Replies
3
Views
2K
MHB Relationship between inner and outer radius of a two concentric circles
Replies
2
Views
2K
MHB Tangent line to circle making 30º with a second circle
Replies
2
Views
2K

Hot Threads

Recent Insights

Back
Top