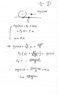A cylinder rolls without slipping

In summary, the conversation discusses a physics homework problem involving a rolling cylinder on a slope. The first part (a) involved calculating the friction force and determining the minimum coefficient of kinetic friction. The second part (b) involved considering torque and force equations for rolling without slipping. There was also a discussion about the direction of the friction force and the possibility of finding the static friction coefficient. The conversation concluded with a clarification on the direction of the friction force and its effect on rotation and translation.
  • #1
athrun200
277
0

Homework Statement


See the attachment Q5

Homework Equations


The Attempt at a Solution


Let's begin with part (a) first.
After finishing this homework (see the second attachment), I suddenly noticed 1 thing. The friction will gradually decrease to zero and then change the direction to become same as the motion direction.
Therefore, my work on part (a) would be wrong. Since I assume the friction is a constant (mgμsinθ).
How do I fix it?

And also, is my way to find the minimum coeff of kinetic friction correct?

And for part (b), it is really that easy?
 

Attachments

  • Q5.jpg
    Q5.jpg
    47.4 KB · Views: 552
  • 2010Q5.jpg
    2010Q5.jpg
    23.3 KB · Views: 482
Physics news on Phys.org
  • #2
For part (a), make sure you use the correct trig functions when finding the components of the weight. Otherwise, looks good!

For part (b), the friction is no longer kinetic friction when rolling without slipping.
 
  • #3
TSny said:
For part (a), make sure you use the correct trig functions when finding the components of the weight. Otherwise, looks good!

For part (b), the friction is no longer kinetic friction when rolling without slipping.
Is it possible to find out the static friction coefficient in this question? Or we can just let a new μ be static friction coefficient?

For part (a), do you mean that the friction would be either kinetic or static, there is not intermediate between them (i.e. the friction would increase or decrease from one to another)?
 
Last edited:
  • #4
Part (a) looks good except for finding the correct expressions for the components of mg along the slope and perpendicular to the slope.

For part (b), you do not need a coefficient of friction. Just consider the torque and force equations and link them using the relation between linear and angular acceleration for rolling without slipping.
 
  • #5
Thank you! I will change the sin and cos!
 
  • #6
Oh, I found that the direction of the friction turns out to be to the left. Does it make sense?
 

Attachments

  • Q5correct.jpg
    Q5correct.jpg
    14.5 KB · Views: 448
  • #7
athrun200 said:
Oh, I found that the direction of the friction turns out to be to the left. Does it make sense?

Before rolling, the cylinder shifts downward so the kinetic friction acts in the opposite direction, upward along the slope. With that direction, friction accelerates rotation and decelerates translation.

ehild
 
  • #8
athrun200 said:
Oh, I found that the direction of the friction turns out to be to the left. Does it make sense?

Yes. There has to be a clockwise torque about the CM in order to give a clockwise angular acceleration as the cylinder accelerates down the slope.
 

1. What does it mean for a cylinder to roll without slipping?

When a cylinder rolls without slipping, it means that the surface of the cylinder is in constant contact with the ground and there is no slipping or sliding motion between the cylinder and the ground. This happens when the linear velocity of the center of the cylinder and the angular velocity of the cylinder are equal, resulting in a smooth and continuous rolling motion.

2. How is the speed of a rolling cylinder calculated?

The speed of a rolling cylinder can be calculated by multiplying the angular velocity (ω) of the cylinder by the radius (r) of the cylinder. This is because the linear velocity (v) of a point on the edge of the cylinder is equal to the product of its angular velocity and its distance from the center (v = ωr). This relationship is known as the tangential velocity.

3. What is the difference between rolling with and without slipping?

Rolling with slipping occurs when the linear velocity and angular velocity of the cylinder are not equal, causing the cylinder to slip or skid on the ground. This can happen if there is insufficient friction between the cylinder and the ground or if external forces are acting on the cylinder. Rolling without slipping, on the other hand, happens when the linear and angular velocities are equal, resulting in a smooth rolling motion without any slipping or sliding.

4. How does the mass of a cylinder affect its rolling motion?

The mass of a cylinder does not directly affect its rolling motion. However, a heavier cylinder may require more force to set it in motion and may have a greater inertia, making it harder to stop once it is rolling. The shape and surface of the cylinder, as well as the friction between the cylinder and the ground, are more significant factors in determining its rolling motion.

5. Can a cylinder roll without slipping on any surface?

In theory, a cylinder can roll without slipping on any surface as long as there is sufficient friction between the cylinder and the surface. However, in practice, the surface roughness and other factors such as the presence of obstacles or inclines can affect the ability of a cylinder to roll without slipping. In general, smoother surfaces with higher friction coefficients are better for achieving rolling without slipping.

Similar threads

Kinetic Energy of a Cylinder Rolling Without Slipping
    • Introductory Physics Homework Help
Replies
21
Views
1K
Question regarding Rolling with and without Slipping and Sliding
    • Introductory Physics Homework Help
Replies
4
Views
1K
Cylinder Rolling Down an Incline Without Slipping
    • Introductory Physics Homework Help
Replies
7
Views
2K
Constraints on a hoop rolling on a cylinder
    • Introductory Physics Homework Help
Replies
1
Views
2K
Motion of Rolling Cylinder in Fixed Cylinder: Confusing Constraint Condition
    • Introductory Physics Homework Help
Replies
2
Views
1K
Finding the time for an object to start rolling without slipping
    • Introductory Physics Homework Help
Replies
4
Views
784
Rolling without slipping, theory
    • Introductory Physics Homework Help
Replies
11
Views
1K
Acceleration of system related to rolling motion and pulley
    • Introductory Physics Homework Help
2
Replies
35
Views
2K
Cylinder rolling on a moving board
    • Introductory Physics Homework Help
Replies
16
Views
2K
Rolling cylinder or slipping cylinder reaches bottom first?
    • Introductory Physics Homework Help
Replies
5
Views
3K

Hot Threads

Recent Insights

Back
Top