maxd23
- 6
- 0
Homework Statement
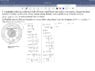
A neutral conducting cylindrical shell with inner radius b and outer radius c surrounds a charged insulated cylinder of radius a at its center whose volume charge density varies radially away from the center as
ρ(r) = ρ0 (1− r / a) . A cross-sectional view is shown.
(a) Find the electric field as a function of r everywhere using Gauss’ Law for 4 regions: (i) 0 < r < a; (ii) a < r < b; (iii) b < r < c; (iv) r > c.
I'm Having trouble with the 4th part (iv) and what the charge on the inner surface of the conductor would be.
Homework Equations
E•dA = Qenc/E_0
The Attempt at a Solution
I have uploaded an image with my work