- #1
erik-the-red
- 89
- 1
Question:
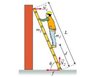
A uniform ladder with mass [tex]m_2[/tex] and length L rests against a smooth wall. A do-it-yourself enthusiast of mass [tex]m_1[/tex] stands on the ladder a distance d from the bottom (measured along the ladder). The ladder makes an angle [tex]\theta[/tex] with the ground. There is no friction between the wall and the ladder, but there is a frictional force of magnitude f between the floor and the ladder. [tex]N_1[/tex] is the magnitude of the normal force exerted by the wall on the ladder, and [tex]N_2[/tex] is the magnitude of the normal force exerted by the ground on the ladder. Throughout the problem, consider counterclockwise torques to be positive. None of your answers should involve [tex]\pi[/tex]. (i.e., simplify your trig functions).
1. What is the minimum coeffecient of static friction [tex]mu_min[/tex] required between the ladder and the ground so that the ladder does not slip?
I'm thinking [tex]f_s + (-n_1) = 0[/tex].
[tex]n_2 + (-9.80m_1) + (-9.80m_2) = 0[/tex]
[tex]n_2 = 9.80(m_1 + m_2)[/tex]
[tex]\sum \tau_B = (n_1)(Lcos(\theta)) - (9.80)(m_1)(d)(cos(\theta)) - (9.80)(m_2)(1/2)(L)(cos(\theta)) = 0[/tex]
[tex]n_1 = (9.80)(dm_1 + (1/2)(Lm_2)/L[/tex] and [tex]f_s=n_1[/tex].
[tex]\mu_s=f_s/f_n[/tex], where [tex]f_s[/tex] is maximum force of static friction.
[tex]\mu_s = (dm_1 + (1/2)(Lm_2))/(L(m_1 + m_2))[/tex].
My answer is not correct. Apparently, I'm missing some trig.
What have I excluded or considered incorrectly?
A uniform ladder with mass [tex]m_2[/tex] and length L rests against a smooth wall. A do-it-yourself enthusiast of mass [tex]m_1[/tex] stands on the ladder a distance d from the bottom (measured along the ladder). The ladder makes an angle [tex]\theta[/tex] with the ground. There is no friction between the wall and the ladder, but there is a frictional force of magnitude f between the floor and the ladder. [tex]N_1[/tex] is the magnitude of the normal force exerted by the wall on the ladder, and [tex]N_2[/tex] is the magnitude of the normal force exerted by the ground on the ladder. Throughout the problem, consider counterclockwise torques to be positive. None of your answers should involve [tex]\pi[/tex]. (i.e., simplify your trig functions).
1. What is the minimum coeffecient of static friction [tex]mu_min[/tex] required between the ladder and the ground so that the ladder does not slip?
I'm thinking [tex]f_s + (-n_1) = 0[/tex].
[tex]n_2 + (-9.80m_1) + (-9.80m_2) = 0[/tex]
[tex]n_2 = 9.80(m_1 + m_2)[/tex]
[tex]\sum \tau_B = (n_1)(Lcos(\theta)) - (9.80)(m_1)(d)(cos(\theta)) - (9.80)(m_2)(1/2)(L)(cos(\theta)) = 0[/tex]
[tex]n_1 = (9.80)(dm_1 + (1/2)(Lm_2)/L[/tex] and [tex]f_s=n_1[/tex].
[tex]\mu_s=f_s/f_n[/tex], where [tex]f_s[/tex] is maximum force of static friction.
[tex]\mu_s = (dm_1 + (1/2)(Lm_2))/(L(m_1 + m_2))[/tex].
My answer is not correct. Apparently, I'm missing some trig.
What have I excluded or considered incorrectly?
Attachments
Last edited: