A Person Standing on a Leaning Ladder

[erik-the-red]

Question:
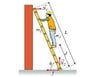
A uniform ladder with mass m_2 and length L rests against a smooth wall. A do-it-yourself enthusiast of mass m_1 stands on the ladder a distance d from the bottom (measured along the ladder). The ladder makes an angle \theta with the ground. There is no friction between the wall and the ladder, but there is a frictional force of magnitude f between the floor and the ladder. N_1 is the magnitude of the normal force exerted by the wall on the ladder, and N_2 is the magnitude of the normal force exerted by the ground on the ladder. Throughout the problem, consider counterclockwise torques to be positive. None of your answers should involve \pi. (i.e., simplify your trig functions).

1. What is the minimum coeffecient of static friction mu_min required between the ladder and the ground so that the ladder does not slip?

I'm thinking f_s + (-n_1) = 0.
n_2 + (-9.80m_1) + (-9.80m_2) = 0
n_2 = 9.80(m_1 + m_2)
\sum \tau_B = (n_1)(Lcos(\theta)) - (9.80)(m_1)(d)(cos(\theta)) - (9.80)(m_2)(1/2)(L)(cos(\theta)) = 0
n_1 = (9.80)(dm_1 + (1/2)(Lm_2)/L and f_s=n_1.
\mu_s=f_s/f_n, where f_s is maximum force of static friction.
\mu_s = (dm_1 + (1/2)(Lm_2))/(L(m_1 + m_2)).

My answer is not correct. Apparently, I'm missing some trig.

What have I excluded or considered incorrectly?

 

[erik-the-red]

Well, I figured out my mistake and I got the right answer.

But, I fell into the "B-Trap" for the second part of this question.

Suppose that the actual coefficent of friction is one and a half times as large as the value of mu_min. That is, \mu_{\rm s} = (3/2)\mu_{\rm min}. Under these circumstances, what is the magnitude of the force of friction f that the floor applies to the ladder?

The ladder is no longer on the verge of slipping. So, f_s = (\mu_s)(n_2) is not correct.

What do I reconsider?

 

[highcoughdrop]

Check this out, it may not help you much, but its something.

 

[tiny-tim]

Check this out, it may not help you much, but its something.

Hi highcoughdrop!

erm … erik-the-red's last activity on this forum was about ten months ago!

 

[highcoughdrop]

Yeah, I'm aware of that, but the only reason I posted anything on here was so that the people who use google to search the physics forums have something when they do find this.

Besides... that's how I got here, lol

 

[shurane]

Awesome, highcoughdrop! That's pretty much how I got here too. You were pretty helpful there, you know.

 

[yandao87]

is the answer for part b same as that for part a? I'm stuck at b. :)

 

[yandao87]

any one can tell me if the answer for part b is the same as part a?
i managed to solve only part a..

 

[gorignak]

Hey if anyone is still having trouble with this, (m_1*d+m_2*L/2)*cos(theta)*g/(L*sin(theta))