ehabmozart
- 212
- 0
Homework Statement
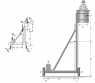
The platform assembly has weight W1 and center of gravity at G1. If it is intended to support a
maximum load W2 placed at point G2,,determine the smallest counterweight W that should be
placed at B in order to prevent the platform from tipping over.
Homework Equations
Equilibrium of rigid bodies
The Attempt at a Solution
Well, the steps are quite easy only if the FBD is drawn correctly... First of all, in the solution given in the second thumbnail, the counterweight points downwards.. Why is it so?? Isn't it COUNTER weight so it points upwards... Anyway, I let it go... Secondly and most importantly, in the solution's approach they equated the moment about D to be 0... As far as I know the 'correct' equation should be
-W2.f + W1.c + WB.(b+c) +Nc.(a+b+c)= 0 ... However, in the book they omit the last part on the left side which is ignoring the normal at C as if it doesn't create any moment about D... Can someone explain this??
Thanks to whoever gives me a kind hand!
Attachments
Last edited: