A small mass on a wedge having a stationary circular track

[Kaushik]

Homework Statement

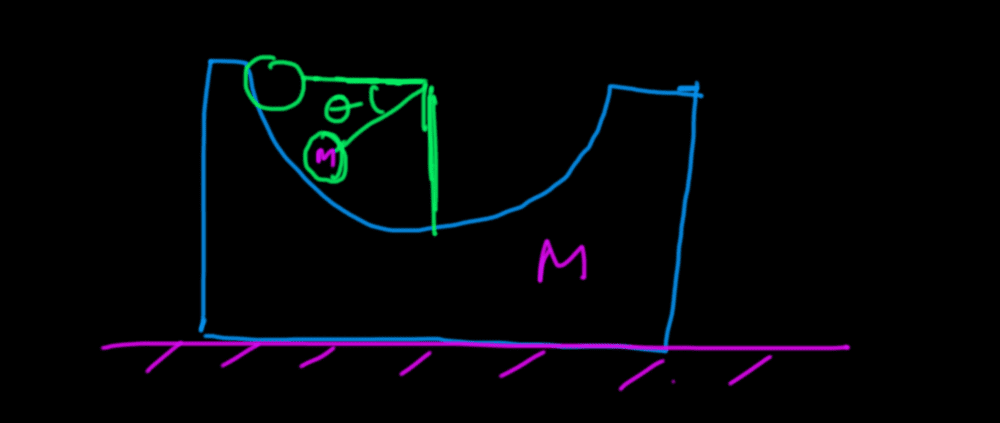
A small mass of $m$ starts sliding down a wedge which is having a stationary circular track on it. If $M = 2m$ and friction exists between the wedge and the horizontal surface. Draw the Frictional force vs Theta graph.

Relevant Equations

Attached

A small mass of $m$ starts sliding down a wedge which is having a stationary circular track on it. If $M = 2m$ and friction exists between the wedge and the horizontal surface. Draw the Frictional force vs Theta graph.

How to draw the graph?

Please HELP

 

[kuruman]

Is the statement of the problem exactly how it was given to you? I am asking because two important questions need be answered
1. Is there friction between mass $m$ and the track?
2. Is the track sliding on the surface?
If the answer is "no" to both questions, then find $v(\theta)$ and then draw a FBD of the track. Use the FBD to find the force of static friction as a function of $\theta$ and then plot it.

 

[haruspex]

Is the track sliding on the surface?

We are told it is stationary.

 

[kuruman]

We are told it is stationary.

Yes, I missed that at first.

 

[Kaushik]

Is the statement of the problem exactly how it was given to you?

This was the exact question. Is it incomplete? There might be some mistake in the question itself.

 

[haruspex]

Yes, I missed that at first.

But then, why give the mass of the wedge? Just to confuse?

 

[haruspex]

This was the exact question. Is it incomplete? There might be some mistake in the question itself.

I would assume the wedge is stationary and there is no friction between it and the mass.
What must be the net force on the mass at the position shown?

 

[Kaushik]

What must be the net force on the mass at the position shown?

Are you asking when it makes 0 degree with the horizontal?
Is it $mg$?

 

[haruspex]

Are you asking when it makes 0 degree with the horizontal?

No, in the diagram position, at angle theta below starting point.

Tension

Tension? Tension in what?

 

[Kaushik]

No, in the diagram position, at angle theta below starting point.

Is it $mgcosΘ$?

Tension? Tension in what?

Sorry, there is no tension acting here.

 

[kuruman]

But then, why give the mass of the wedge? Just to confuse?

Perhaps to draw an upper limit in the graph assuming a $\mu_s$ or maybe this probelm is derived from an incompletely modified earlier version in which the wedge was free to move on a frictionless table and one was asked for a plot of the wedge's displacement vs. angle.

 

[jbriggs444]

Is it $mgcosΘ$?

Please show your work. What leads you to guess $m g \cos \theta$? Have you drawn a free body diagram? For what object? Have you accounted for the acceleration of the ball in its track?

Edit: Expanding a bit on this.

When we look at the classic situation of a block sliding down an inclined plane, one can use a coordinate system lined up with the diagonal surface of the plane. In this coordinate system the acceleration on the y-axis (perpendicular to the plane) is zero. If follows that one can equate the normal force on the block from the plane to the y component of gravity: $F = m g \cos \theta$.

This holds because the acceleration in the perpendicular direction is zero. The two forces have to sum to zero.

But we do not have a flat inclined plane. In the case at hand, is the acceleration perpendicular to the curved surface equal to zero?

 

[Kaushik]

But we do not have a flat inclined plane. In the case at hand, is the acceleration perpendicular to the curved surface equal to zero?

The $Normal$ provides the centripetal acceleration.

 

[haruspex]

The $Normal$ provides the centripetal acceleration.

The net of all forces normal to the surface provides the centripetal acceleration. The "normal force" from the wedge is not the only contribution.

 

[Kaushik]

The net of all forces normal to the surface provides the centripetal acceleration. The "normal force" from the wedge is not the only contribution.

The only forces that are normal to the surface at angle $\theta$ are Normal and $mg\sin(\theta)$. Am I correct?

 

[haruspex]

The only forces that are normal to the surface at angle $\theta$ are Normal and $mg\sin(\theta)$. Am I correct?

Yes.

 

[Kaushik]

Yes.

Now should I draw the FBD of the wedge?

 

[kuruman]

Now should I draw the FBD of the wedge?

Yes.