A Square Loop of Wire falling through a Magnetic Field

[TFM]

Homework Statement

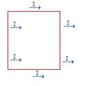
A vertical square loop of copper wire with sides of length 100 mm is falling from a region where the magnetic field is horizontal and of magnitude 1.2 T into a region where the field is zero, as shown in the diagram below. The diameter of the copper wire is 1 mm.
[The resistivity of copper is $$1.7 x 10^{-8} \Ohm$$ m; the density of copper is 8960 kg m-3.]

(i) Calculate the magnitude of the current round the loop, in terms of the velocity of fall v, and indicate its sense.

(ii) What is the magnetic force acting on the loop, again expressed in terms of v?

(iii) If the velocity of fall reaches a steady value whilst the upper arm of the circuit remains in the field, calculate this velocity.

Homework Equations

V = IR
$$R = \rho \frac{l}{A}$$
$$\epsilon = -\frac{d\Phi_B}{dt}$$
$$\Phi = BA$$

The Attempt at a Solution

Okay I am on the first part I have calculated the Current like so:

Area of each 'side' = 0.001 x 0.1 = 0.0001m x 4 sides = 0.0004m^2

$$\Phi_B = 1.2 * 0.0004 = 0.00048$$

$$\epsilon = -\frac{\Delta\Phi_B}{\Delta T} = \frac{0.00048}{\frac{0.1}{v}} = 0.0048v$$

V = IR:

I = V/R, using
$$R = \rho \frac{l}{A}$$

l = 0.4m
A = $$\pi * (0.0005)^2 = 7.85 * 10^{-7}$$

$$R = 1.7 * 10^{-8}zfrac{0.4}{7.85 * 10^{-7}} = 8.66 * 10^{-3} \Ohms$$

$$I = \frac{V}{R} = \frac{0.0048v}{8.66 * 10^{-5}} = 0.554v Amps$$

The thing I am uncertain on at the moment is what is the sense? I haven't heard of this term before?

Any ideas?

TFM

 

[chrisk]

The force on a charge is related to the relative velocity of the charge and the magnetic field by

$$\vec{F}=q\vec{v}\times\vec{B}$$

This will give you the sense or direction of the current.

 

[TFM]

Okay, so using the left hand rule, with the V going down and the B field going into the screen/page, I get that the Current will be going to the right. Does this seem reasonable, because it is a loop, so surely the current will need to travel around the loop, or does it mean that the current is going right through the whole loop, i.e. the attached Diagram?

 

[chrisk]

A current is produced when the wire cuts the lines of magnetic flux. So, only two sections of the wire will have an induced EMF. Again, use qv x B which is also equal to il x B where i is the current in the wire and l is the length of the conductor cutting the lines of B.

 

[TFM]

Okay, so the current will be running downwards?

 

[chrisk]

First, consider the force on the free charge in the top wire and the bottom wire (the charges in the side wires do not experience a force from the B field because these two wires do not cut lines of magnetic flux). When the entire loop is in the B field, what is the net force? Then when the bottom wire enters the zero B field what is the net force? Another way to look at it is using your definitions for EMF. In order for an EMF to occur there has to be a change in the magnetic flux linking the loop with respect to time. What is the change in B when the loop is completely in the B field? What is the change in B when the loop begins to exit the B field? Hint: how is the area of the loop exposed to the B field changing?

 

[TFM]

Well, when the loop is entirely in the B field, the net force will be 0, because you need a change in B-Field to produce a force. The change in B will be -1.2T. The loop will be exposed to the changing B field by firstly having a change on the bottom 'side', then along the to up-down 'sides', and then finally along the to 'side'.

 

[chrisk]

The area of the loop exposed to the B field changes as a function of the velocity. Use this to calculate the EMF as a function of v. And yes, while the entire loop is in the B field, the current is zero because there's no change in the magnetic flux.

 

[TFM]

Okay, so:

$$\epsilon = -\frac{d\Phi_B}{dt}$$

Area of each 'side' = 0.001 x 0.1 = 0.0001m x 2 sides = 0.0002m^2

$$\Phi_B = 0.0002* 1.2 = 0.00024$$

$$\epsilon = -\frac{\Delta\Phi_B}{\Delta t} = -\frac{0.00024}{0.1/v} = -\frac{0.00024v}{0.1} = 0.0024v Volts$$

Using:

$$R = 1.7 * 10^{-8}\frac{0.4}{7.85 * 10^{-7}} = 8.66 * 10^{-3} \Ohms$$

Gives the Current to be:

$$I = \frac{V}{R} = \frac{0.0024v}{8.66 * 10^{-5}} = 0.277v Amps$$

Does this look okay?

 

[chrisk]

$$EMF= -\frac{d\Phi_B}{dt}$$

and

$$\frac{dA}{dt}=l\frac{dx}{dt}=-lv$$

$$\Phi = BA$$

So,

$$EMF = Bvl$$

when the loop starts to exit the uniform B field. The value l is the length of a side of the square loop.

 

[TFM]

Okay, i never thought about breaking down the da into l dx.

So:

$$\epsilon = Bvl = 1.2*v*0.001 = 0.0012v Volts$$

Turning this onto current:

$$I = \frac{v}{R} = \frac{0.0012v}{8.66 * 10^{-3}} = 0.139v Amps$$

Does this look better for the current?

 

[chrisk]

The expression is correct. Check the value of l in the expression. The units should be meters.

 

[TFM]

Okay, should have been 0.1m

This Makes the EMF 0.12v Volts, and hence the Current 13.9 Amps.

So the Sense of the current is its direction, and is given by F = qv x B, and I assume that it is the qv part, but which direction would the force be acting?

 

[chrisk]

Try Lenz' Law (right hand rule curling the fingers in the direction of B) to determine the direction of the current. The current produced in the wire that is cutting the B field will create its own B field that will oppose the movement of the loop. Using F = qv x B, the force, F, on the charge is the cross product of the direction and magnitude of the charge and B. If you define current as the direction of electron movement then use -q. If your definition of current is the movement of holes (positive charges) then use q.

You can also use

F = il x B

where the force, F, will point up (opposing the motion of the loop according to Lenz' Law) and since the direction of B is known, the direction of i (current) can be determined in the wire cutting the B field. Again, this direction is for holes.

 

[TFM]

Okay, so using the left-hand rule, with
F = il x B,

B is goping int page, and F is going up to oppose motion, so

The holes are going to the right, electrons to the left

Does this seem okay?

 

[chrisk]

Using the right hand rule (this applies to cross products) the positive charge is accelerated to the right. Your use of the left hand rule gives the same direction. Therefore, the current sense is clockwise with respect to the viewer.

 

[TFM]

Using the right hand rule (this applies to cross products) the positive charge is accelerated to the right. Your use of the left hand rule gives the same direction. Therefore, the current sense is clockwise with respect to the viewer.

Wouldn't the Left hand rule give the opposite direction, not the same?

 

[chrisk]

Wouldn't the Left hand rule give the opposite direction, not the same?

Yes, in a left handed coordinate system. A right hand coordinate system is generally used.

 

[TFM]

Fair enough, but hoe comes the Right Hand rule, which I thought was three fingers all perpendicular to each other like so:

[URL]http://en.wikipedia.org/wiki/File:Right_hand_rule_cross_product.svg

So how do we get a circular motion instead?

 

[chrisk]

Because the EMF is a force and accelerates the electrons in the wire segment falling through the B field to the left. The holes move the other way and this is the direction of the current around the loop. Recall, when the entire loop was in the field no current existed. This is because the current induced in the lower wire was in the same direction and the two currents cancel each other.

 

[TFM]

I think I see now...The lectrons move to the right, but the whole system is moving downards, so the lectrons appear to move in a arc. Does this meak sense?

 

[chrisk]

No, this does not make sense. Think of it this way; the EMF produced in the top wire is like a battery. The three other sections of the loop are the conductors with a resistance, which you calculated. The V you determined is the voltage of the "battery".

 

[TFM]

I see so basically when the wire goes down, it has an EMF which induces a current which then travels around the the loop.

 

[chrisk]

Yes, you got it.

 

[TFM]

Excellent.

So now for the second part, I ahve to find the force due to the magnetic field. I assume I need to use:

F = il x B,

Which, since they are perpendicular, can reduce to:

F = IlB

Giving the force to be:

F = 13.9*0.1*1.2

Giving the force to be 1.67 Newtons?

 

[chrisk]

Yes, you seem to have it now. You're on your own!

 

[TFM]

Okay then. I don't seem to get the last question, though:

If the velocity of fall reaches a steady value whilst the upper arm of the circuit remains in the field, calculate this velocity.

I am not sure for this question. Are we assuming it has reached terminal velocity, so it has been dropped for some time, or is there something else to do?

 

[chrisk]

Use Lenz' Law and equate to mg. It is not the terminal velocity of freefall in a zero B field.

 

[TFM]

Okay, so I assume we make the Force we just calculated - mg, like thus:

BIl = mg

1.67v = 9.8m, and I assume we work out the mass using the volume and diameter...?

 

[chrisk]

Check out this site. It has a good explanation of the type of problem you are working on.

www.physics.smu.edu/~vega/em1304/lectures/lect13/lect13_f03.ppt[/URL]

 

[TFM]

A good link, Thanks

so for the velocity:

1.67v = mg

$$v = \frac{mg}{1.67}$$

$$m = vol*\rho$$

$$v = \frac{vol \rho g}{1.67}$$

the volume is:

$$4*(length of side*area) = 4(0.1*\pi * 0.0005^2) = \pi * 10^{-6}$$

$$v = \frac{\pi * 10^{-6} (8960) (9.8)}{1.67}$$

this gives v to be: 0.165 m/s

Seems rather small?

 

[chrisk]

Your answer is correct. 1.2 Tesla is a HUGE B field and the mass of the wire is very small.

 

[TFM]

1.2 T is a large field, so I suppose the speed would be slow.

Thanks for all your assistance, chrisk, most appreciated

Thanks

TFM