vkash
- 316
- 1
A vessel filled with two liquid how to determine boyant force?
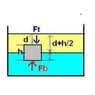
A vessel contains oil of density(800kgm-3) over mercury (density 13600kgm-3) A homogeneous Sphere is floats with half of its volume immersed in mercury and other half in oil. What is density of the material of the sphere?
How to apply Archimedes principle of floating? can you please help.
A vessel contains oil of density(800kgm-3) over mercury (density 13600kgm-3) A homogeneous Sphere is floats with half of its volume immersed in mercury and other half in oil. What is density of the material of the sphere?
How to apply Archimedes principle of floating? can you please help.
Last edited: