snoopies622
- 852
- 29
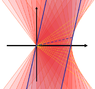
Consider the upper half of the hyperbola
<br /> <br /> (ct)^2 - x^2 = a^2<br /> <br />
where a^2 is a positive constant. The spacetime distance between any point on this curve and the origin is the positive number a. A thought experiment helps give this some physical meaning to me: If I'm at x=0 with a set of identical clocks, and at time = 0 I simultaneously throw them all at different speeds along the x-axis, then the time on every clock when it hits the curve will be the same (a).
Now consider the right half of the hyperbola
<br /> <br /> (ct)^2 - x^2 = b^2<br /> <br />
where b^2 is a negative constant. The spacetime distance between any point on this curve and the origin is also a constant, but I don't know of an analogous thought experiment to help give this hyperbola physical meaning.
Any suggestions?
<br /> <br /> (ct)^2 - x^2 = a^2<br /> <br />
where a^2 is a positive constant. The spacetime distance between any point on this curve and the origin is the positive number a. A thought experiment helps give this some physical meaning to me: If I'm at x=0 with a set of identical clocks, and at time = 0 I simultaneously throw them all at different speeds along the x-axis, then the time on every clock when it hits the curve will be the same (a).
Now consider the right half of the hyperbola
<br /> <br /> (ct)^2 - x^2 = b^2<br /> <br />
where b^2 is a negative constant. The spacetime distance between any point on this curve and the origin is also a constant, but I don't know of an analogous thought experiment to help give this hyperbola physical meaning.
Any suggestions?