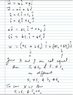Abstract Vector Basis: Necessary & Sufficient Condition for Plane Representation

[PcumP_Ravenclaw]

Homework Statement

Suppose that $u = s_1i + s_2j$ and $v = t_1i + t_2j$, where s1, s2, t1 and t2 are real
numbers. Find a necessary and sufficient condition on these real numbers
such that every vector in the plane of i and j can be expressed as a linear
combination of the vectors u and v.

Homework Equations

We shall need to consider directed line segments, and we denote the directed
line segment from the point a to the point b by [a, b]. Specifically, [a, b] is the
set of points {a + t(b − a) : 0 ≤ t ≤ 1},

The Attempt at a Solution

As attached.

 

[BvU]

Phrase it this way: if $\vec w = x \; \hat\imath + y \; \hat \jmath$ then what do you have to do to write it as $\vec w = a \; \vec u + b\; \vec v$ ?
When can you do that and when can you not do that ?

 

[PcumP_Ravenclaw]

Phrase it this way: if $\vec w = x \; \hat\imath + y \; \hat \jmath$ then what do you have to do to write it as $\vec w = a \; \vec u + b\; \vec v$ ?
When can you do that and when can you not do that ?

$\vec u = s_1 \vec i+ s_2 \vec j$

$\vec v = t_1 \vec i+ t_2 \vec j$

$x = a s_1 + b t_1$

$y = a s_2 + b t_2$

 

[Mark44]

$\vec u = s_1 \vec i+ s_2 \vec j$

$\vec v = t_1 \vec i+ t_2 \vec j$

$x = a s_1 + b t_1$

$y = a s_2 + b t_2$

Is it always possible to solve for a and b? What if u or v is the zero vector? What if u and v are equal? What if u is a nonzero multiple of v?

You have a very simple space here -- the plane. The question boils down to this: what does it take for two vectors to span a plane?

 

[BvU]

$\vec u = s_1 \vec i+ s_2 \vec j$

$\vec v = t_1 \vec i+ t_2 \vec j$

$x = a s_1 + b t_1$

$y = a s_2 + b t_2$

So, try to solve for a and b and see what you get !

 

[PcumP_Ravenclaw]

I believe I have only found two/three cases that restrict the coefficients of u and v. I have attached my solution.

 

[BvU]

Solving for a and b means you express the unknowns a and b in terms of the knowns, x, y, s₁, s₂, t₁ and t₂.