- #1
The Count
- 27
- 0
- TL;DR Summary
- Which values takes the third and forth derivative of distances in universe? Acceleration needs third derivative at least positive. Dark energy as is most considered now leads to increasing third derivative.
Since distances increase, their first derivative which is velocity (Hubble constant) should be positive if not increasing too. Accelerated expansion needs the velocity to increase. What about the third derivative which is acceleration? An accelerated universe could have third derivative (called jerk) constant positive, increasing positive or even decreasing positive, even going to zero gradually. I made a quick graph table that shows what I am talking about.
Dark energy, by increasing with space (voids) as is most considered now, leads to increasing second derivative and possibly positive constant third derivative. Do we have any clue by observational data about these?
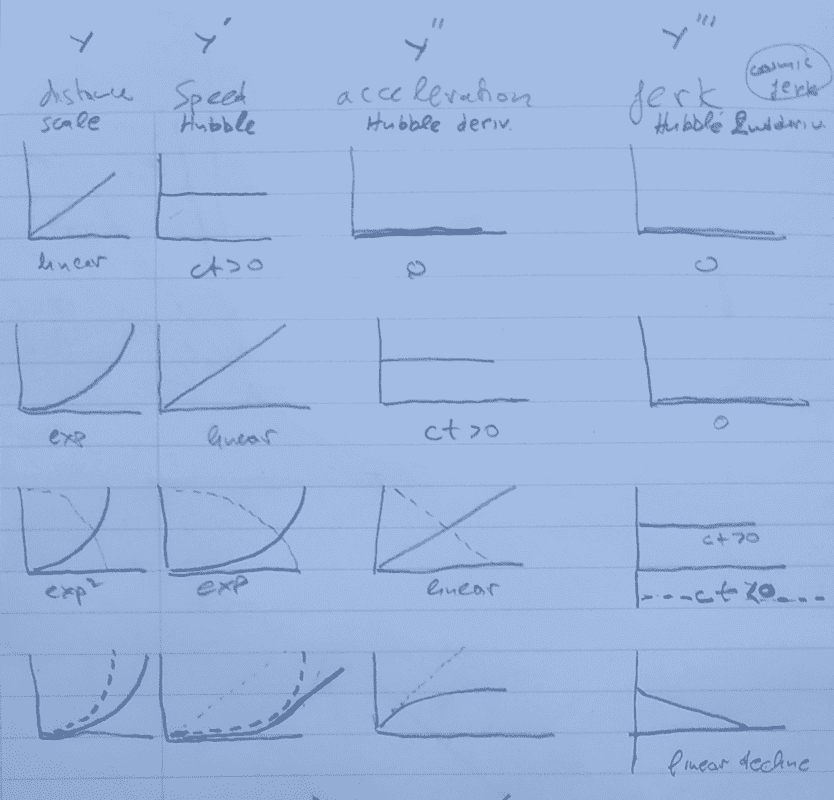
Dark energy, by increasing with space (voids) as is most considered now, leads to increasing second derivative and possibly positive constant third derivative. Do we have any clue by observational data about these?