Accelerating an inclined plane

[syang9]

hello,

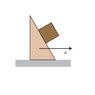
consider an plane inclined at an angle theta with a block on it. the problem asks me to find a horizontal acceleration such that the block will not slide down the plane.
in part (a), friction is neglected, in part(b), friction is considered.

here is what i have done. i fixed the coordinate system so that the force of the push applied to the inclined plane is in the x-direction.

(a): Fnetx = Fnx (normal force in x direction) + Fp (force of push) = 0
Fnety = Fny + Fg = 0

solving for Fp, i get Fp = Fn(cos(theta)). this seems reasonable, but too easy. have i left something out?

(b): considering friction, i have fixed the coordinate system as in part a.

Fnetx = Fp + Fnx -Ffx (force of friction in x direction) = 0
Fnety = Fg + Ffy +Fny = 0

solving for Fp, i get Fp = -Fn(sin(theta))*(1-μs) (μs = coefficient of static friction) however, there should be a minimum and a maximum force.. the minimum force is with maximum friction, and the maximum force is the force that force that is on the verge of accelerating the block in the negative x direction. or am i wrong? have i left something out? i am pretty sure i have.

any help is greatly appreciated. (i have attached a picture of the problem)

 

[Doc Al]

here is what i have done. i fixed the coordinate system so that the force of the push applied to the inclined plane is in the x-direction.

(a): Fnetx = Fnx (normal force in x direction) + Fp (force of push) = 0
Fnety = Fny + Fg = 0

solving for Fp, i get Fp = Fn(cos(theta)). this seems reasonable, but too easy. have i left something out?

I assume you are analyzing the forces on the block. If so, two comments:

(1) The only forces acting on the block are weight and the normal force. What do you mean by Fp? (Note that the question asks for the acceleration, not the force on the plane that would produce such acceleration. Although once you have "a", it's easy to find "F".)

(2) Why do you assume equilibrium in the horizontal direction? After all, the question asks for the acceleration.​

Hint: If the block doesn't slide down the plane it must be in vertical equilibrium.