Accelerating Wedge and block on top of it -- Dynamics

[andyrk]

Homework Statement

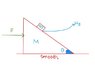
In the figure a block of mass 'm' is placed on a wedge of mass M. The wedge is subject to a horizontal force 'F' and slides on a friction less surface. The coefficient of static friction between the block and wedge is μ_s. Find the range of values of 'F' for which the block does not slide on the incline.

Homework Equations

If the bodies (block+wedge) move together then:
F=(M+m)a

The Attempt at a Solution

If 'F' is too less, then the block of mass 'm' will have a tendency to come down the incline.
If 'F' is too much, the block will have a tendency to move up the incline.
So 'F' need to be in between these minimum and maximum values and that's how we get the range. But my doubt is that why do the above 2 conditions i.e when F is too less and when F is too much happen?

 

[haruspex]

why do the above 2 conditions i.e when F is too less and when F is too much happen?

Why or when? Are you able to write out and solve the equations?
Note that in the case of sliding down, it may be that F needs to go negative if the angle is low or the friction is high.

 

[andyrk]

"When" is the statement itself..That is , the 2 respective cases happen when their respective conditions are met. Namely, F being very less or very large. My question is for the "why" part. As to does the block specifically move upwards when F is too large? If it moves up there has to be some force acting up the incline..how does that force arise, i.e the force that makes the block move up the incline when F is too large? Is it because of a pseudo force that we have included, opposite to the acceleration of the (wedge+block) since this system is an accelerating one with respect to an inertial frame namely us or the ground? If that happens then we can resolve this pseudo acceleration into two components, and one those components acts up the incline so the block moves up the incline. But then, are we considering ourselves or the ground as the frame of reference or the system itself as the frame of reference?
The thing is I maybe having the answers to my queries but I am just too doubtful to accept my answer..

 

[Tanya Sharma]

Is it because of a pseudo force that we have included, opposite to the acceleration of the (wedge+block) since this system is an accelerating one with respect to an inertial frame namely us or the ground? If that happens then we can resolve this pseudo acceleration into two components, and one those components acts up the incline so the block moves up the incline.

Hi andyrk

The component of pseudo force acts up the incline,whereas the component of weight acts down the incline.In case the component of pseudo force is greater than the component of weight then the block has the tendency to move up.Hence friction acts downwards.In case the former is less than the latter ,the block has the tendency to slide down.So,friction acts upwards.

But then, are we considering ourselves or the ground as the frame of reference or the system itself as the frame of reference?

Since we are applying pseudo force ,we are surely working from the accelerated frame of reference,i.e the wedge .The observations are made from the wedge ,not the ground.

 

[andyrk]

What are the observations that we are making from the frame of reference of the (block+wedge) system?

 

[Tanya Sharma]

What
are the
observations that we are making from the frame of reference of the
(block+wedge) system?

The frame of reference is wedge ,not wedge+block.The block is seen sliding up,stationary,sliding down the wedge depending on the force applied to the wedge.

 

[andyrk]

Oops..yeah sorry my bad

 

[andyrk]

Hi andyrk

The component of pseudo force acts up the incline,whereas the component of weight acts down the incline.In case the component of pseudo force is greater than the component of weight then the block has the tendency to move up.Hence friction acts downwards.In case the former is less than the latter ,the block has the tendency to slide down.So,friction acts upwards.
Since we are applying pseudo force ,we are surely working from the accelerated frame of reference,i.e the wedge .The observations are made from the wedge ,not the ground.

Can the reason for why the block moves up the incline and down the incline be explained without using pseudo force method and just normal application of Newton's Second Law?

 

[haruspex]

Can the reason for why the block moves up the incline and down the incline be explained without using pseudo force method and just normal application of Newton's Second Law?

Of course. Applied corectly, inertial frames and non-inertial frames should lead to the same answer. It's only a question of which is more convenient.

 

[andyrk]

Of course. Applied corectly, inertial frames and non-inertial frames should lead to the same answer. It's only a question of which is more convenient.

So how would one do that? I am not able to think of an explanation without using Pseudo Force which explains why the block moves up or down the incline depending on the magnitude of the force.

 

[haruspex]

So how would one do that? I am not able to think of an explanation without using Pseudo Force which explains why the block moves up or down the incline depending on the magnitude of the force.

Down the incline is ok, yes? If little force is applied and the friction is weak it will slide down.
For the block to slide up the incline, it is only required that the horizontal acceleration of the wedge exceeds that of the block. We can make the wedge accelerate as fast as we like by applying a large enough force. The acceleration of the block in that direction depends on the normal force from the wedge (limited by g) and the frictional force (limited by g and mu).

 

[andyrk]

Down the incline is ok, yes? If little force is applied and the friction is weak it will slide down.
For the block to slide up the incline, it is only required that the horizontal acceleration of the wedge exceeds that of the block. We can make the wedge accelerate as fast as we like by applying a large enough force. The acceleration of the block in that direction depends on the normal force from the wedge (limited by g) and the frictional force (limited by g and mu).

So even if the wedge accelerates faster than the block, why would the block move upwards?

 

[haruspex]

So even if the wedge accelerates faster than the block, why would the block accelerate upwards?

Because the only other option is for it to penetrate the block.

 

[andyrk]

Because the only other option is for it to penetrate the block.

Yep. That makes some sense intuitively. But can we explain it a bit more quantitatively rather than qualitatively?

 

[andyrk]

Anybody there?

 

[haruspex]

Yep. That makes some sense intuitively. But can we explain it a bit more quantitatively rather than qualitatively?

I had the impression you were after a qualitative explanation.
To go quantitative, write some equations.

 

[andyrk]

I had the impression you were after a qualitative explanation.
To go quantitative, write some equations.

I did. But I was unable to find a reasonable explanation for this without including pseudo forces in. How do you do that?

 

[haruspex]

I did. But I was unable to find a reasonable explanation for this without including pseudo forces in. How do you do that?

You have the acceleration. Suppose it is on the point of slipping up the plane. Put in an unknown for the normal force. What equations do you get?

 

[andyrk]

The equations for the block are: Rcosθ = mg and Rsinθ = mA, where A is the acceleration of the block+wedge system.
This is for the case when the block is at rest (assuming that it is).
When it is not, what proof do we have that it moves upwards when the force is a lot and it moves downwards when the force is low? How can we be sure this is going to happen? I know it seems right intuitively and by using pseudo forces we can even prove it. But can we prove it without intuition and pseudo forces?

 

[haruspex]

The equations for the block are: Rcosθ = mg and Rsinθ = mA, where A is the acceleration of the block+wedge system.
This is for the case when the block is at rest (assuming that it is).
When it is not, what proof do we have that it moves upwards when the force is a lot and it moves downwards when the force is low? How can we be sure this is going to happen? I know it seems right intuitively and by using pseudo forces we can even prove it. But can we prove it without intuition and pseudo forces?

Where R is the normal force? You've left out friction.

 

[andyrk]

Friction comes into play when the block slides. But why would it slide in the first place?

 

[haruspex]

Friction comes into play when the block slides. But why would it slide in the first place?

Static friction applies well before the block slides.
Here's the plan:
Three unknowns, normal force N, friction Ff, acceleration a.
Three equations, horizontal F=ma for the wdge, horizontal and vertical for the block.
Solve to find Ff/N as a function of M, m, F, theta and g.

 

[TSny]

Can the reason for why the block moves up the incline and down the incline be explained without using pseudo force method and just normal application of Newton's Second Law?

For simplicity, consider the case where there is no friction. If the force F applied to the wedge is large enough the block will slide up the incline. But note that in the inertial frame, the block slides horizontally in the same direction as the wedge while it also has a vertical component of displacement. Considering the directions of the two forces acting on the block, it should not be too surprising that the block can move this way.

 

[andyrk]

For simplicity, consider the case where there is no friction. If the force F applied to the wedge is large enough the block will slide up the incline. But note that in the inertial frame, the block slides horizontally in the same direction as the wedge while it also has a vertical component of displacement. Considering the directions of the two forces acting on the block, it should not be too surprising that the block can move this way.

Why does it have a vertical component of displacement?

 

[TSny]

The normal force on the block has a vertically upward component. If the applied force F on the wedge is increased, what do you suppose happens to the magnitude of the normal force on the block? What happens when the vertical component of the normal force exceeds the weight of the block?

 

[andyrk]

The normal force on the block has a vertically upward component. If the applied force F on the wedge is increased, what do you suppose happens to the magnitude of the normal force on the block? What happens when the vertical component of the normal force exceeds the weight of the block?

The block flies off and leaves contact with the wedge. But still, we don't have any force along to incline to make it slide upward or downward. And anyway, the normal force would never exceed the weight because normal force is by definition always equal to the force with which the block is pressing against the wedge.

 

[haruspex]

The block flies off and leaves contact with the wedge. But still, we don't have any force along to incline to make it slide upward or downward. And anyway, the normal force would never exceed the weight because normal force is by definition always equal to the force with which the block is pressing against the wedge.

The normal force can exceed the weight because of the acceleration. The only way to settle this is with equations. Have another go at them.

 

[TSny]

The block flies off and leaves contact with the wedge...And anyway, the normal force would never exceed the weight because normal force is by definition always equal to the force with which the block is pressing against the wedge.

The block does not leave contact with the wedge. When you stand in an elevator that accelerates upward, the upward normal force on you is greater than your weight. But you don't lose contact with the floor. (The elevator accelerates with you.)

But still, we don't have any force along to incline to make it slide upward or downward.

There does not need to be any force component upward along the incline in order for the block to increase its height on the wedge. If you vectorially add the normal force and weight, you get a net force on the block that points upward and to the right (if the normal force is sufficiently large). So the block accelerates upward and to the right while remaining on the wedge, as shown in the figure I previously posted. If you add in the friction force, you should still be able to see how it is possible for the block to increase its height while remaining on the wedge.

But I think I might be detracting from the main point of setting up and working through the equations.

 

[andyrk]

The equations are: Ncosθ = mg and Nsinθ = mA. None of these forces are along the incline so how can the block slide up or down the incline?

 

[TSny]

The equations are: Ncosθ = mg and Nsinθ = mA. None of these forces are along the incline so how can the block slide up or down the incline?

Since there is no friction force in these equations, we must still be considering the case of no friction.

When you write Ncosθ = mg, you are assuming at the outset that the block will have no vertical acceleration. In that case, the block can naturally remain in one place on the incline and not slide up or down the incline as the wedge is pushed. But, note that Ncosθ = mg tells you what N must be for this to happen. Using this value of N in your second equation will determine the specific value of A that must occur in this case. From that you can get the specific force F that needs to be applied to the wedge so that the block will not slide up or down the frictionless incline. So, only if you push the wedge with this one specific value of F will the block not slide up or down the incline. If F is greater than this specific force, the block will slide up the incline; if less, it will slide down.