aaronfue
- 118
- 0
Homework Statement
I believe that I have my answer. I would appreciate it if someone could check my work.
m1 = 33 kg
m2 = 14 kg
μ = 0.19
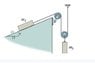
Angle is given by 5,12,23 triangle shown in figure.
Assume pulleys are massless.
What is the acceleration of mass m2 on the incline plane? (Positive acceleration to be up ramp)
Homework Equations
Mass 2:
T - m2g(\frac{5}{13}) - μm2g(\frac{12}{13}) = m2a2
Mass 1:
2T - m1g = m1a1
Pulley System:
a2 = -2a1
The Attempt at a Solution
Even though acceleration is assumed to be up the ramp, I drew my FBD with acceleration going down the ramp. I know that if my answer is negative it will be the opposite direction of what I assumed.
After I plugged the pulley equation into the mass 2 equation and then solved two equations with two unknowns:
T = 279.8 N
a1 = 7.15 \frac{m}{s^2}
a2 = 14.30 \frac{m}{s^2} (Initially this was a negative answer, which reversed my assumption of the direction)