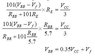SUMMARY
The discussion focuses on algebraic manipulation techniques to solve complex equations involving voltage and resistance in electrical circuits. The key takeaway is that by equating two expressions that are both equal to VCC/3, one can derive RBB as a constant multiple of RE. Substituting this relationship into the initial equations yields the desired expression involving VBB, Vf, and VCC. The participant successfully resolved their confusion by following this systematic approach.
PREREQUISITES
- Understanding of electrical circuit theory
- Familiarity with Ohm's Law and voltage division
- Basic algebraic manipulation skills
- Knowledge of circuit components such as resistors and voltage sources
NEXT STEPS
- Study the principles of voltage division in electrical circuits
- Learn advanced algebraic techniques for manipulating equations
- Explore circuit analysis methods using Kirchhoff's laws
- Investigate the relationship between resistors in series and parallel configurations
USEFUL FOR
Electrical engineering students, circuit designers, and anyone involved in solving complex equations related to electrical circuits will benefit from this discussion.