Algebraic Vectors - Calculating Unit Vectors and Magnitudes

[dekoi]

edit // 1-4 have been answered. Please scroll down.
-----
Firstly, i would like to make sure whether i am clear on this subject.

If A is (2, 3, 5) and B (5, 2, -3), would AB equal (3, -1, -8) ? And the magnitude of AB would be the Square.root(9+1+64+ .

Either way, i would like someone to assist me in these problems.

1.) "Find the components of the unit vector with direction opposite to that of the vector from X(7,4,-2) to Y(1,2,1)

I first figured out XY, which is (6, -2, 3). Am i correct to assume the opposite of this XY is (-6, 2, -3) ? I then used the formula for the unit vector calculation to figure out the coordinates of the unit vector.However, my answer was (-6/7, 2/7, -3/7) -- while the correct answer should be (6/7, 2/7, 3/7).

2.) ABCDEF is a regular hexagon with sides of unit length. Find the magnitude of direction of AB + AC + AD + AE + AF (all vectors). ABCDEF is drawn counter-clockwise (for conveniance).

I first made AF = AB. Therefore, 2AB + AC +AD + AE. Then AE = AC. Therefore, 2AB + 2AC + AD. Now, am i correct to say AD = AB + BC + CD ? The rest i should be able to calculate.

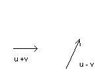
3.) The sum and the difference of two vectors u and v are given. Show how to find the vectors themselves.

See attached image for Diagram.

I am completely stuck on this one. Is there a proper way of doing it, without trial and error?

4.) Find the length of the median AM in the triangle ABC, for the points A (2, 3/2, -4), B (3, -4, 2), and C (1, 3, -7).

Once again, would e.g AB equal x2 - x1, y2-y1, z2-z1 ?


Thank you.
Please repond asap.

 

[dav2008]

Firstly, i would like to make sure whether i am clear on this subject.

If A is (2, 3, 5) and B (5, 2, -3), would AB equal (3, -1, -8) ?

Edit: I realized that you're trying to find the vector between 2 points and not the product of two vectors, but here is the info anyway if you need it
There are two types of vector multiplication: vector(or cross) product and scalar(or dot) product.

Cross(vector) Product is written as <a, b, c> x <d, e, f> and it yields a new vector

The new vector is the determinant of the matrix
| i j k |
| a b c |
| d e f |

Dot(scalar) product is written as <a, b, c> _{\scriptsize \bullet} <d, e, f> and it yields a scalar.

To solve a dot product you multiply the corresponding components and then add them up. (a*d + b*d + c*f)

(Note that for the dot product you technically do multiply a*e and a*f but since those components are perpendicular their product is 0)

 

[Galileo]

If A is (2, 3, 5) and B (5, 2, -3), would AB equal (3, -1, -8) ?

From your post I think you mean AB to be the 'vector from A to B'. Then yes, but it's just B-A. The notation AB is usually used for multiplication (dot or cross-products of vectors).

1.) "Find the components of the unit vector with direction opposite to that of the vector from X(7,4,-2) to Y(1,2,1)

I first figured out XY, which is (6, -2, 3).

The vector from X to Y should be Y-X=(-6,-2,3). You got the length right and the opposite direction is obtained by multiplying the vector by -1.

3.) The sum and the difference of two vectors u and v are given. Show how to find the vectors themselves.

This is general algebra, not for vectors in particular.
If
x+y=a and
x-y=b
Then adding and subtracting these equations give:
2x=a+b and
2y=a-b
respectively.

 

[dekoi]

Thank you for the responses. I have figured out all the questions/answers.

One more question however, for:

4.) Find the length of the median AM in the triangle ABC, for the points A (2, 3/2, -4), B (3, -4, 2), and C (1, 3, -7).

I have calculated AM.
However, part B is as follows:

Find AX, X being the centroid of the triangle (all medians intersect at centroid).

Does anyone have any ideas? I am not really knowledgeable of any properties involving the centroid of a triangle.

One idea i have: Is the centroid two-thirds the distance to the opposite side on the median. I am fairly sure this is true. Therefore, M1X is 2/3 of M1B (M1 being midpoint, X the centroid, and B as the vertex). Is there a name for this property. Or is it just a definition of a centroid?


Thank you again.

 

[dekoi]

Is the centroid two-thirds the distance to the opposite side on the median. I am fairly sure this is true. Therefore, M1X is 2/3 of M1B (M1 being midpoint, X the centroid, and B as the vertex). Is there a name for this property. Or is it just a definition of a centroid?

Thank you again.

Would anyone happen to know?

 

[nelufar]

Thank you for the responses. I have figured out all the questions/answers.

One more question however, for:

4.) Find the length of the median AM in the triangle ABC, for the points A (2, 3/2, -4), B (3, -4, 2), and C (1, 3, -7).

I have calculated AM.
However, part B is as follows:

Find AX, X being the centroid of the triangle (all medians intersect at centroid).

Does anyone have any ideas? I am not really knowledgeable of any properties involving the centroid of a triangle.

One idea i have: Is the centroid two-thirds the distance to the opposite side on the median. I am fairly sure this is true. Therefore, M1X is 2/3 of M1B (M1 being midpoint, X the centroid, and B as the vertex). Is there a name for this property. Or is it just a definition of a centroid?


Thank you again.

Since you have calculated AM, you can calculate AX. X is the centroid and centroid divides the median (median AM) in the ratio 2:1. So, you can say AX is 2/3 of AM.