I Am I crazy or is my book wrong?

[yjl]

Hey all,

My book says/does the following.

Use the following equation for a plane wave

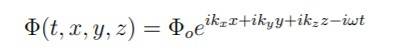
Fill it in the klein-gordon equation

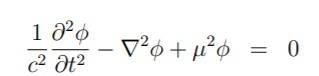
To get

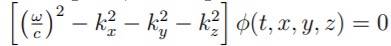
Which results in

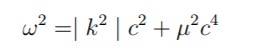
Is this right? I got something different and no matter how hard I try I can't replicate the same answer. I've gotten the last equation, but without the c to the power of 4. I also feel like they just flat out forgot μ in the third equation.

 

[jasonRF]

I've gotten the last equation, but without the c to the power of 4.

It should be $\omega^2 = c^2 k^2 + c^2 \mu^2$, where $k^2 = k_x^2 + k_y^2 + k_z^2$; if this is what you got then you did it correctly

I also feel like they just flat out forgot μ in the third equation.

Yes.

By the way, what book is this?

Jason

 

[yjl]

It should be $\omega^2 = c^2 k^2 + c^2 \mu^2$, where $k^2 = k_x^2 + k_y^2 + k_z^2$; if this is what you got then you did it correctly

Yes.

By the way, what book is this?

Jason

Yes, thank you!

That's what I kept ending up on. :-)

It's not a book that's publicly available. It's my professor's LaTeX book that he wrote for the course. He did say that it's still very much a work in progress, but still..

 

[jtbell]

It's my professor's LaTeX book that he wrote for the course

I hope you'll tell him about this, politely. If it were me, I would appreciate the feedback.

 

[yjl]

I hope you'll tell him about this, politely. If it were me, I would appreciate the feedback.

Yes, I e-mailed him. Wonder if he'll appreciate or find it annoying to be honest

 

[ZapperZ]

Yes, I e-mailed him. Wonder if he'll appreciate or find it annoying to be honest

If he finds it annoying that someone pointed out a mistake in his text, then he has no business being a physicist, or an educator for that matter.

Zz.