An electron moving across capacitor

[spatel600]

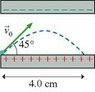
An electron is launched at a 45 angle and a speed of 5.0*10^6 from the positive plate of the parallel-plate capacitor shown in the figure. The electron lands 4.0 cm away.

What is the electric field strength inside the capacitor?


What is the minimum spacing between the plates?


So what I have put together so far is that a=(q*E)/m but what does E equal to. Then once I have acceleration it becomes a kinematics.


Please help! Thanks so much

 

[chroot]

The acceleration is found via the Lorentz force law and Newton's second law. Once you have the acceleration, as you say, it's just kinematics. It sounds like you have this one already figured out -- where exactly are you getting stuck?

- Warren

 

[spatel600]

We haven't covered Lorentz force law.

Any more tips?

Thanks a bunch.

 

[chroot]

The Lorentz force law is:

\mathbf{F} = q \mathbf{E} + \mathbf{v} \times \mathbf{B}

When the magnetic field is zero, it reduces to just

\mathbf{F} = q \mathbf{E}

Given the electric field strength, all you need to do to find the force on a particle is multiply by the particle's charge.

- Warren

 

[spatel600]

But what is the E field...its not given...


Any input?


Thanks.

 

[spatel600]

This what i have so far:
(x)t = Vox * t
t=1.14*10^-7 seconds
I broke up the v0 into xy components v0x=3.5*10^5
v0y=3.5*10^5

The problem now is that

F=qE =
a=qE/m
I don't know the acceleration nor the E so this is where i am stuck at


PLEASE HELP!


THANKS SO MUCH

 

[chroot]

Do you not have a book? All of the things you're asking should be in it, probably even indexed.

The electron begins with a vertical (upward) velocity of v_{0y} = (5 \cdot 10^6~\textrm{m/s}) / \sqrt{2} = 3.5 \cdot 10^6~\textrm{m/s}, and a horizontal (rightward) velocity of the same magnitude, as you found.

The electric field is perpendicular to the plate, so it affects only the vertical motion, not the horizontal motion -- just like gravity.

The electron traveled 4.0 cm at its constant horizontal velocity. That took

t = \frac{0.04 \textrm m \cdot \sqrt{2}}{5 \cdot 10^6~\textrm{m/s}} = 11.31 \cdot 10^{-9}~\textrm{s}

During that 11.31 nanosecond period, the electron's altitude above the plane went from zero, up to some maximal value, and back to zero again. The standard kinematic equation you need is

s(t) = v_0 t + \frac{1}{2} a t^2

Plug in the initial vertical velocity and solve for the acceleration.

Now that you have the acceleration, you can use Newton's second law to get the force.

Now that you have the force, you can use the Lorentz force law (\mathbf F = q \mathbf E) to get the E field.

The second part of the question is just asking you to the find the maximum altitude the electron gains above the plate. This is another basic kinematic result:

y_\textrm{max} = \frac{v_{0y}}{2a}

- Warren

 

[robphy]

Think about the kinematics problem first.
Hint: Can you find the acceleration somehow?

Once you have acceleration, you can (using F=ma) find E since you already know (or can look up) the charge and mass of the electron.

To answer the last part, you might want to look at the kinematics problem again.

 

[spatel600]

Thanks so much guys, I really appreciate it!
!