- #1
kl055
- 26
- 0
Homework Statement
Homework Equations
Superposition
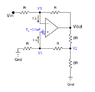
Non-inverting OPAMP: V_out = (1 + R/R)V_in = 2*V_in2
Inverting OPAMP: V_out = -V_in
V_os = 2.5mV
The Attempt at a Solution
1. V_in enabled, V_os disabled
V_out1 = -V_in
2. V_os enabled, V_in disabled
To get V_out2, use the non inv. equation where V_in2 is equal to V_1 + V_os
where V_1 is the node between R and R at the middle bottom of the circuit.
V_out2 = 2*(V_1 + V_os)
3. V_out = V_out1 + V_out2
Is this the correct approach?
Thanks in advance :)
Last edited: