ramz
- 13
- 0
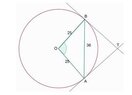
View attachment 4819
Hi everyone, I need further explanations about the answer of this problem.
The answer is angle T = 87.9 degrees.
Thanks.
Hi everyone, I need further explanations about the answer of this problem.
The answer is angle T = 87.9 degrees.
Thanks.